הרצאה 6 – אנליזה ווקטוריתאנליזה ווקטורית פונקציה ווקטורית היא פונקציה
מהצורה הגדרה - הדיברגנץ יהי נפח סופי V, ויהי המשטח הסוגר עליו S. נחלק את הנפח לנפחים קטנים הווקטור
הדיברגנץ נקרא גם "צפיפות השטף של השדה". הדיברגנץ
מוגדר בכל נקודה במחרב ש- משפט גאוס (המתמטי) יהי נפח סופי V, ויהי המשטח הסוגר עליו S, אזי: כאשר משמעות הביטוי חזרה – משפט גאוס (הפיסיקלי) יהי נפח סופי V, ויהי המשטח הסוגר עליו S, אזי: מסקנות מחוק גאוס החוק מקשר למעשה בין הדיברגנץ למקורות השדה. אם האופרטור נבלה תזכורת: האופרטור נבלה מוגדר כך: הצגת הדיברגנץ בקורדינטות קרטזיות בקורדינטות קרטזיות, מתקיים:
נוכל לרשום את הדיברגנץ גם בצורה הבאה: צורת כתיבה זו נכונה לא רק לגבי מערכת צירים קרטזיות, אם כי במערכות צירים אחרות, האופרטור נבלה מוגדר בצורה שונה. משפט סטוקס, סירקולציה, curl
הגדרה צפיפות (משטחית) של הסירקולציה
בכיוון הווקטור
משפט סטוקס:
S הינו משטח חלק ופתוח ששפתו C. כיוון ההליכה על C: נלך על מסלול כך שנראה את המשטח מצד שמאל. כיוון הראש הוא כיוון הנורמל (כלל הבורג – סיבוב בורג ימני). curl בקורדינטות קרטזיות:
מסקנות ממשפט סטוקס ראשית, נסכם את המשפט בצורה הבאה:
כמו כן: curl שווה אפס אם השדה החשמלי משמר, ומספר שונה מאפס אם לא. |
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


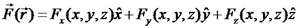 .
.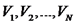 ואת המשטח למשטחים הסוגרים על הנפחים
ואת המשטח למשטחים הסוגרים על הנפחים 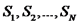 בהתאמה.
בהתאמה.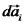 הוא ווקטור שגודלו כגודל השטח
הוא ווקטור שגודלו כגודל השטח 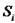 וכיוונו ככיוון האנך כלפי חוץ לאותו אלמנט שטח.
וכיוונו ככיוון האנך כלפי חוץ לאותו אלמנט שטח.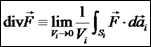
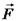 מוגדרת בו.
מוגדרת בו.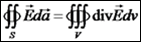
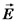 שדה ווקטורי כלשהו.
שדה ווקטורי כלשהו. 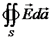 היא השטף של הווקטור
היא השטף של הווקטור 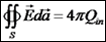 , כאשר
, כאשר 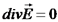 , אזי אין מקורות, ואם
, אזי אין מקורות, ואם 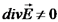 יש מקורות. חוסר מקורות: האם יש מקורות לשדה בנפח שאנו כולאים, לא
האם יש מקורות לשדה בכלל.
יש מקורות. חוסר מקורות: האם יש מקורות לשדה בנפח שאנו כולאים, לא
האם יש מקורות לשדה בכלל.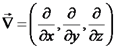
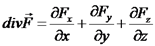
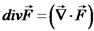
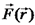 ומסלול סגור במרחב C.
ומסלול סגור במרחב C.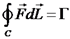 .
.
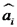 :
: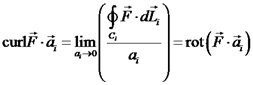
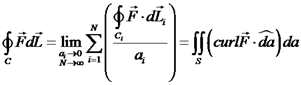
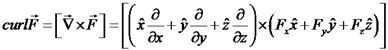
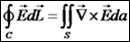
תיקון על התאבכות של N סדקים
כתבת בהערה השנייה שיש יותר מינימות מאשר מקסימות אך זה לא נכון (מכיוון שהפונקציה גזירה...), בין כל 2 מקסימות יש מינימה ובין כל 2 מינימות יש מקסימה.