תרגול 3הגדרה הלפלסיאן יוגדר כך:
תרגיל
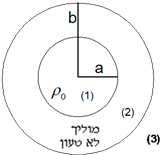
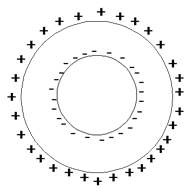
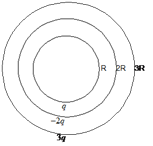
נתון גוף מבודד טעון, ומסביבו מוליך לא טעון. נרצה למצוא את השדה ואת הפוטנציאל ב- (1), (2) וב-(3). כללים
הערות על הכללים לגבי 1, לכאורה הפוטנציאל בנקודה מסויימת תלוי רק במטען באותה נקודה. עובדה זו אכן נכונה, ומתקבלת מפיתוח המשוואה. לגבי 3, נשים לב שמדובר על השדה השקול בכל נקודה, ולא רק
בשדה הנובע מהמטען בנקודה זו.
נעשה אינטגרל לשני האגפים:
חשוב לא לפספס את הוספת הקבוע.
כעת אנו יכולים לדעת מהו
מהסימטריה ידוע כי
עבור (2)
כאשר עבור (3)
מכיוון ש-
ידוע כי הפוטנציאל באינסוף הוא 0, ולכן:
השדה:
נרצה כעת להיפטר מהקבועים. נשתמש ברציפות הפוטנציאל:
השדה על פני המוליך הינו כמו כן: כעת נחלץ את הקבועים מהמשוואות.
שאלה נוספת: נרצה כעת לחשב את האנרגיה הכללית האצורה במערכת:
תרגילים תרגיל 1
תרגיל 2 קליפה כדורית מוליכה בעלת רדיוס מחברים את שתי הקליפות בחוט מוליך דק. נדרש לחשב את הפוטנציאל של שתי הקליפות. המטען מתפצל לשני מטענים, מתקיים:
הפוטנציאל:
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


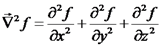
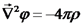 .
.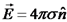 .
.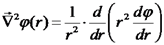
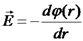
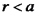 :
: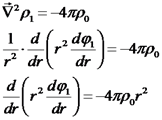
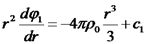
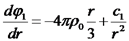
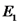 :
: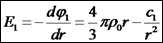
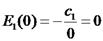 , ולכן מתקיים כי
, ולכן מתקיים כי 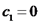
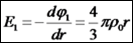
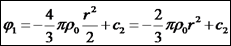
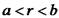 :
: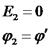
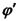 הינו קבוע.
הינו קבוע.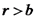 :
: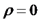 , מתקיים כי
, מתקיים כי 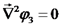 .
.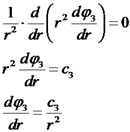
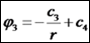
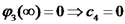
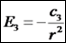
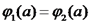 .
.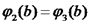
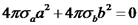
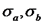 הן צפיפויות המטען המשטחיות על שפות המוליך.
הן צפיפויות המטען המשטחיות על שפות המוליך.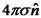 , והוא שווה לשדה השקול בנקודה. השדה הינו
, והוא שווה לשדה השקול בנקודה. השדה הינו 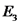 . ומכאן:
. ומכאן: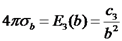
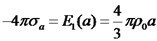
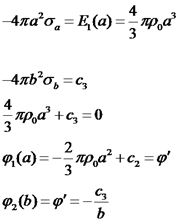
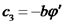
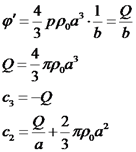
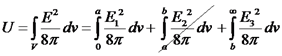
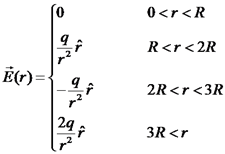
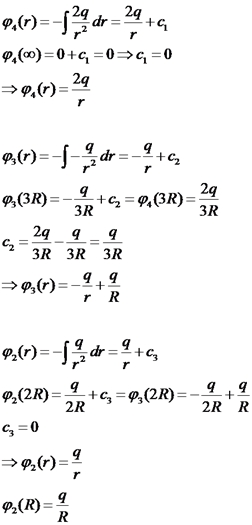
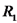 טעונה במטען Q. במרחק d ממנה נמצאת קליפה כדורית לא
טעונה בעלת רדיוס
טעונה במטען Q. במרחק d ממנה נמצאת קליפה כדורית לא
טעונה בעלת רדיוס 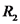 . נתון כי
. נתון כי 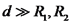 .
.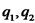 , כאשר אנו מחברים את הקליפות בחוט.
, כאשר אנו מחברים את הקליפות בחוט.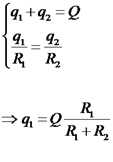
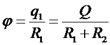
תיקון על התאבכות של N סדקים
כתבת בהערה השנייה שיש יותר מינימות מאשר מקסימות אך זה לא נכון (מכיוון שהפונקציה גזירה...), בין כל 2 מקסימות יש מינימה ובין כל 2 מינימות יש מקסימה.