הרצאה 23 – גלים אלקטרומגנטיים, משוואות מקסוול בריק, משוואת הגלים הקלאסית, גלים במערכות מכאניותגלים אלקטרומגנטיים משוואות מקסוול בריק משווואות מקסוול מובילות אל משוואת הגלים הקלאסית (בריק).
בריק, מחוץ למקורות השדות השונים, מתקיים:
כיצד יתכנו שדות חשמליים ומגנטיים ללא מקורות? התשובה: ישנם
מקורות שדה, אולם אנו מתעלמים מהם, ומסתכלים בריק באיזור מחוץ למערכות שם מתקיים
כי משוואת הגלים הקלאסית אנו למעשה מחפשים את
נפתח את המכפלה הווקטורית ונקבל את משוואת הגלים הקלאסית
עבור נדגיש כי משוואה זו היא למעשה שלוש משוואות:
בצורה דומה נקבל את משוואת הגלים הקלאסית עבור נעיר כי שילמנו מחיר מסוים כאשר השגנו את משוואות הגלים:
ניתקנו את הקשר בין נפתח כעת פיתוחים עבור גלים. רוב הפיתוחים ייעשו עבור גלים מכניים מכיוון שקל יותר להתרגל כך לנושא הגלים. נניח לאחר מכן שהתוצאות נכונות גם עבור גלים אלקטרומגנטיים. גלים במערכות מכניות גל זוהי הפרעה של תווך (מדיום) המקיימת את משוואת הגלים הקלאסית. נוכל לדבר על הפרעות שונות: הפרעה סקלרית כאשר נעסוק בגלים, נפריד בין בעיות על פי סוג התווך וסוג ההפרעה. נבחין כי תווך יכול להיות חד ממדי, בזמן שלהפרעה יהיה יותר ממימד אחד. כאשר נעסוק בתווך חד ממדי, נקבע את ציר להפרעה הנמשכת זמן קצר בלבד נקרא פולס. כאשר ההפרעה הינה בכיוון התקדמות התווך נקרא לה הפרעה אורכית. כאשר ההפרעה הינה בניצב לכיוון התקדמות התווך נקרא לה הפרעה רוחבית. יתכן גם שגל אחד יורכב גם מהפרעה אורכית וגם מהפרעה רוחבית. משוואת הגלים הקלאסית לתווך חד ממדי והפרעה סקלרית נבחר תווך המשתרע לאורך ציר z. כמו כן תהי הפרעה סקלרית נאמר שהפרעה היא גל אם היא מקיימת את המשוואה הבאה:
כאשר v זוהי מהירות הפאזה. משוואה זו היא הצורה הפשוטה ביותר של משוואת הגלים הקלאסית (מכיון שאנו דנים בתווך חד ממדי, ובהפרעה סקלרית בלבד).
משוואת הגלים הקלאסית למיתר אינסופי ותנועה רוחבית בכיוון אחד
המיתר מתוח - במצב של שיווי משקל, על כל במיתר פועל אותו כוח בכיוונים הפוכים. המתיחות היסודית היא קירוב: המתיחות לאורך כיוון
על אלמנט המיתר שאורכו
נשתמש בחוק השני של ניוטון:
ההפרעה שראינו היא למעשה הפרעה ווקטורית, אבל יש לה רק רכיב אחד, ולכן אנו מתייחסים אליה כאל הפרעה סקלרית.
פתרונות של משוואת הגלים הקלאסית שני סוגים של פתרונות: א. גל רץ (תווך אינסופי): נקבל פתרון מהצורה הבאה: נוכיח כי פונקציה זו מהווה פתרון:
ומכאן בצורה דומה ניתן לומר כי גם
פונקציה זו מתארת הפרעה שמתקדמת על ציר z במהירות שחושבה. זהו גל רץ. דוגמא פרטית לגל רץ: גל הרמוני גל הרמוני: כאשר:
זמן מחזור: אין צורך להוכיח ישירות כי הגל ההרמוני מקיים את משוואת הגלים, מכיוון שהוא מקרה פרטי של המשוואה שמצאנו קודם. אורך הגל יוגדר להיות מחזוריות במקום (
מחזוריות בזמן נתונה על ידי:
תנאי הכרחי לקיומו של גל רץ: מערכת פתוחה. הערות
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


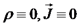 . לפיכך, אנו יכולים לכתוב את משוואות מקסוול בריק בצורה הבאה:
. לפיכך, אנו יכולים לכתוב את משוואות מקסוול בריק בצורה הבאה: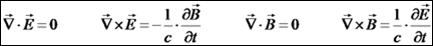
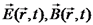 . לפתרון שנמצא נקרא גל. נגזור שוב את משוואות מקסוול:
. לפתרון שנמצא נקרא גל. נגזור שוב את משוואות מקסוול: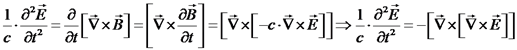
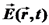 :
: 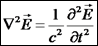
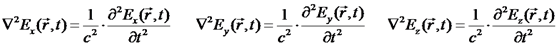
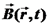 :
: 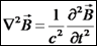
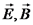 כגלים.
כגלים. 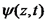 , הפרעה ווקטורית בתווך חד ממדי
, הפרעה ווקטורית בתווך חד ממדי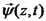 , הפרעה סקלרית בתווך תלת ממדי
, הפרעה סקלרית בתווך תלת ממדי 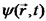 . בשם משדר, נכנה את הכוח שיוצר את ההפרעה
הגלית.
. בשם משדר, נכנה את הכוח שיוצר את ההפרעה
הגלית.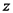 להיות בכיוון התווך. (דוגמא לתווך חד ממדי היא קפיץ
המחובר לקיר).
להיות בכיוון התווך. (דוגמא לתווך חד ממדי היא קפיץ
המחובר לקיר).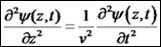
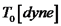 . נניח שההפרעה ממצב שיווי משקל היא בסדר גודל קטן ביחס למיתר,
כלומר, המיתר לא משתנה את אורכו בזמן התנועה. למיתר צפיפות מסה אחידה:
. נניח שההפרעה ממצב שיווי משקל היא בסדר גודל קטן ביחס למיתר,
כלומר, המיתר לא משתנה את אורכו בזמן התנועה. למיתר צפיפות מסה אחידה: 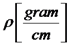 .
.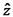 (על הקטע
(על הקטע 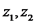 ) נשמרת והיא
) נשמרת והיא 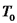 .
.
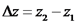 ומסתו
ומסתו 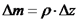 פועל כוח בכיוון רוחבי
פועל כוח בכיוון רוחבי 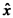 :
: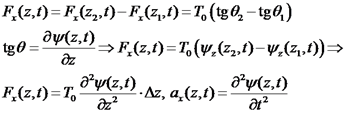
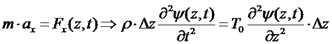
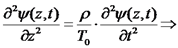
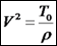
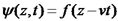 , כאשר
, כאשר 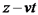 = פאזה.
= פאזה.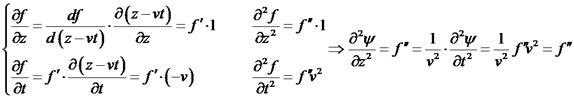
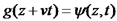 פונקצית גל.
פונקצית גל.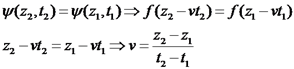
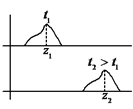
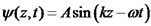 ,
, 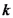 (קבוע) - מספר הגל
(קבוע) - מספר הגל 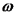 (קבוע) - תדירות זוויתית A (קבוע)
- אמפליטודה
(קבוע) - תדירות זוויתית A (קבוע)
- אמפליטודה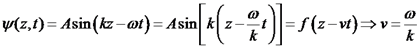
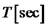 תדירות:
תדירות: 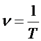 תדירות
זוויתית:
תדירות
זוויתית: 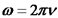
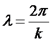 וזהו המרחק בין כל שתי נקודות אקויולנטיות של הגל.
וזהו המרחק בין כל שתי נקודות אקויולנטיות של הגל.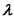 :
: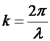
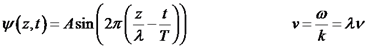
תיקון על התאבכות של N סדקים
כתבת בהערה השנייה שיש יותר מינימות מאשר מקסימות אך זה לא נכון (מכיוון שהפונקציה גזירה...), בין כל 2 מקסימות יש מינימה ובין כל 2 מינימות יש מקסימה.