הרצאה 16 – כוח המופעל על מטען ממקורות נעים, תכונות השדה המגנטי הנובע מזרמים קבועים, הפוטנציאל המגנטיכוח המופעל על מטען q ממקורות נעים
נגדיל את הקטע
בקטע
הכוח פרופורציוני למכפלת הזרמים חלקי המרחק ביניהם. תכונות השדה המגנטי הנובע מזרמים קבועים נקבל את תכונות השדה המגנטי משדה של תיל ישר. נניח כי
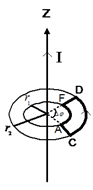
מהי הסירקולציה על מסלול שאינו מקיף את התיל נושא הזרם? ניקח מסלול לדוגמא ונבדוק זאת.
קיבלנו שהסירקולציה על מסלול שאינו מקיף את התיל נושא הזרם היא אפס. הרחבת חוק אמפר נתונים מספר מעגלי זרם במרחב. נבחר מסלול סגור כלשהו חוק אמפר להתפלגות נפחית של זרמים
C - מסלול סגור המהווה את השפה של S.
נשים לב שניתן במקרה זה להשתמש במשפט סטוקס: מכאן נגיע למסקנה כי האינטגרל נכון לכל משטח שהוא, ומכאן גם האינטגרנדים שווים. נקבל את חוק אמפר בצורה דיפרנציאלית: נמצא כעת גם את חוק השטף בצורה דיפרנציאלית. כזכור, השטף של נשתמש במשפט גאוס: מכאן נקבל את חוק השטף בצורה דיפרנציאלית: הקבלה מתמטית בין תכונות השדה החשמלי לבין תכונות השדה המגנטי
נשים לב שהכוח המגנטי הוא חוק שימור האנרגיה מתקיים באופן טריויאלי עבור הכוח המגנטי:
הערה חשובה היא שחוק אמפר איננו חוק שימור האנרגיה. חוק אמפר
מקשר בין חוקי הייסוד לשדה חשמלי ושדה מגנטי בצורה דיפרנציאלית
הפוטנציאל המגנטי תזכורת עבור שדה חשמלי מתקיים כי באופן כללי לגמרי, בהנחה שהתפלגות המטענים היא בעלת גודל
סופי: כעת נשתמש בשתי משוואות הייסוד של השדה המגנטי כדי לקבל ביטוי
מקביל לזה שקיבלנו עבור השדה החשמלי. הפוטנציאל המגנטי (הנקרא גם פוטנציאל
ווקטורי) יסומן ב- בהקבלה ל-(*),
נבחר כי נבדוק כי הבחירה מקיימת את המשוואות היסודיות:
תזכורת: במקרה שלנו:
נזכור כי פונקצית הפוטנציאל הסקלרית מוגדרת עד כדי קבוע.
במקרה של פוטנציאל ווקטורי, נוכל לבחור שרירותית את
זוהי משוואת פואסון לפונקציה ווקטורית עבור הפוטנציאל
הווקטורי |
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |
|||||||||||||||||||||||||||||||||||||||||||||


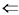 מקור הכוח מהווה מערכת נטראלית.
מקור הכוח מהווה מערכת נטראלית.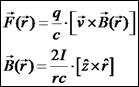
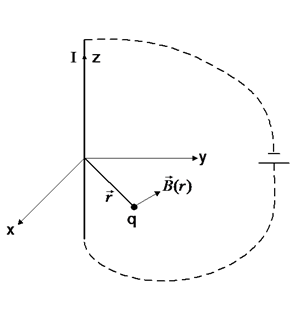
 מפעיל על
מפעיל על  ?
?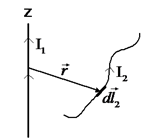
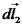 :
:
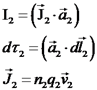
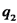 אחד:
אחד: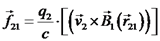
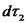 ישנם
ישנם 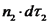 נושאי מטען.
נושאי מטען.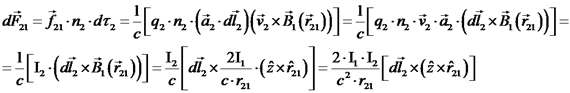
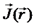 איננו תלוי בזמן t.
איננו תלוי בזמן t.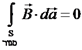
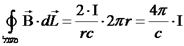
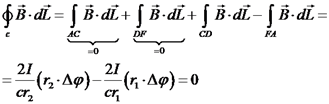
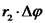 הינו אורך החוט, וכן
הינו אורך החוט, וכן 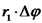
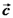 . מעקרון הסופרפוזיציה של שדות נקבל כי
. מעקרון הסופרפוזיציה של שדות נקבל כי 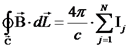 . הסכום הינו סכום אלגברי (עם סימן) של הזרמים.
. הסכום הינו סכום אלגברי (עם סימן) של הזרמים.
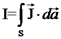 .
.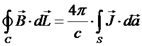
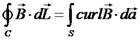 .
.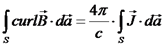 .
.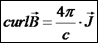
 :
: 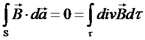 .
.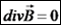
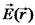
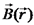
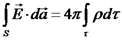
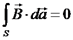
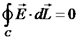
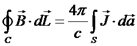
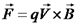 .
. 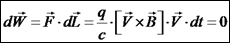
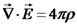
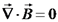
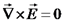
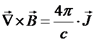
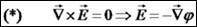 , כאשר
, כאשר 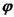 היא פונקצית פוטנציאל סקלרית.
היא פונקצית פוטנציאל סקלרית.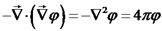 , וכך קיבלנו את משוואת פואסון:
, וכך קיבלנו את משוואת פואסון: 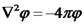 .
.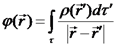 .
.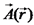 .
.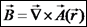 .
.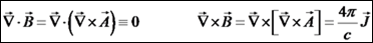
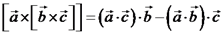 .
.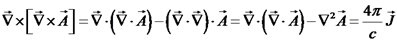
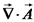 להיות אפס, ואז נקבל:
להיות אפס, ואז נקבל: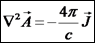
תיקון על התאבכות של N סדקים
כתבת בהערה השנייה שיש יותר מינימות מאשר מקסימות אך זה לא נכון (מכיוון שהפונקציה גזירה...), בין כל 2 מקסימות יש מינימה ובין כל 2 מינימות יש מקסימה.