הרצאה 22 – השראה אלקטרומגנטית ומשוואות מקסוולהשראה אלקטרומגנטית ומשוואות מקסוול הקדמה - פיתוח המשוואות כאשר נשתמש במשפט סטוקס, ונקבל: סיכום חוקי היסוד עבור השדה החשמלי והשדה המגנטי, כפי שהיו ידועים עד מקסוול
התיקון של מקסוול למשוואות היסוד: משוואות מקסוול
מינוח של מקסוול: זרם ההעתק יוגדר משוואת הרציפות של הזרם: עקב זהות ווקטורית, מתקיים:
זרם ההעתק כאשר השדה החשמלי משתנה, אנו יכולים להסתכל על הווקטור דוגמא לחשיבות תיקון מקסוול (זרם ההעתק) קבל טעון במטען 1. נבצע צירקולציה של
2. נבצע צירקולציה של
בין לוחות הקבל
נשים לב שללא תוספת זרם ההעתק, היו מתקבלות תוצאות שונות, בסתירה לחוק אמפר. טענה
הוכחה נחשב את הזרם על מעטפת כדור ברדיוס r.
נחשב את המטען בתוך הכדור - אינטגרל על נפח הכדור:
ומכאן, עבור התפלגות זרמים רדיאלית, מתקיים:
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


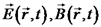 משתנים בזמן (כלומר - מקורות השדות משתנים בזמן) אז לכל מסלול
סגור C ולכל משטח פתוח S (גם בריק) מתקיים כי:
משתנים בזמן (כלומר - מקורות השדות משתנים בזמן) אז לכל מסלול
סגור C ולכל משטח פתוח S (גם בריק) מתקיים כי: 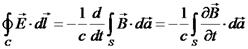 (פארדיי).
(פארדיי).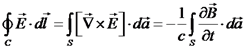 , ונקבל את חוק פארדיי בצורה דיפרנציאלית:
, ונקבל את חוק פארדיי בצורה דיפרנציאלית: 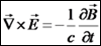 .
.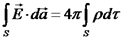
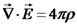
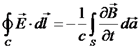
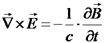
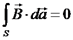
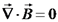
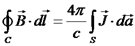
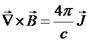
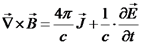 .
.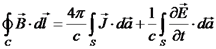
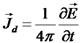 . ומכאן
. ומכאן 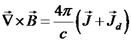
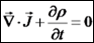
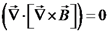 . לפי התיקון נקבל כי
. לפי התיקון נקבל כי 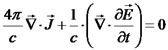 נשתמש בחוק ביו-סבר:
נשתמש בחוק ביו-סבר: 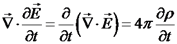 , ונקבל:
, ונקבל: 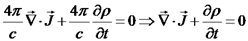
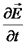 . נביט ביחידות של ווקטור זה.
. נביט ביחידות של ווקטור זה. 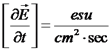 . יחידות אלו זהות ליחידות של צפיפות הזרם. מתקיים:
. יחידות אלו זהות ליחידות של צפיפות הזרם. מתקיים: 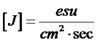 . לפיכך - ניתן להתייחס לגודל זה כאל המשך התפלגות
הזרם.
. לפיכך - ניתן להתייחס לגודל זה כאל המשך התפלגות
הזרם.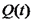 מתפרק דרך מעגל זרם. בקירוב: קבל לוחות טעון המתפרק דרך תיל ישר
אינסופי. כיוון התיל יבחר להיות
מתפרק דרך מעגל זרם. בקירוב: קבל לוחות טעון המתפרק דרך תיל ישר
אינסופי. כיוון התיל יבחר להיות 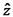 , ואילו הקבל על מישור
, ואילו הקבל על מישור 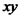 . לכל נקודה במרחב, השדה המגנטי הינו
. לכל נקודה במרחב, השדה המגנטי הינו 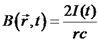 . בין לוחות הקבל קיים גם שדה חשמלי. השדה החשמלי בין הלוחות הינו
. בין לוחות הקבל קיים גם שדה חשמלי. השדה החשמלי בין הלוחות הינו 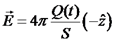 . כעת:
. כעת: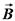 על מסלול מעגלי ניצב לתיל ומחוץ לקבל:
על מסלול מעגלי ניצב לתיל ומחוץ לקבל: 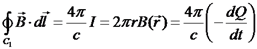
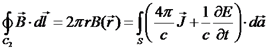
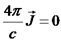 .
.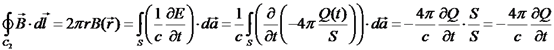
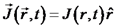 , אזי יתקיים כי
, אזי יתקיים כי 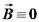 .
.
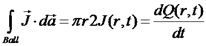
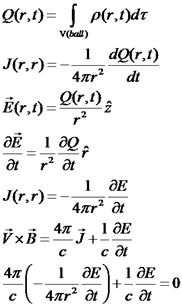
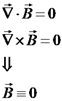
תיקון על התאבכות של N סדקים
כתבת בהערה השנייה שיש יותר מינימות מאשר מקסימות אך זה לא נכון (מכיוון שהפונקציה גזירה...), בין כל 2 מקסימות יש מינימה ובין כל 2 מינימות יש מקסימה.