הרצאה 24 – גל עומד, גלים במרחב ובמישורב. גל עומד במערכת סגורה (סופית) כל נקודה זזה באמפליטודה קבועה, אם כי לכל נקודה תיתכן אמפליטודה משלה. דוגמא מיתר מוחזק בשני קצותיו. פתרון של גל עומד (הרמוני): בגל רץ הפאזה (תוכן הסינוס) הוא קומבינציה ליניארית של פונקציה של המקום ופונקציה של הזמן. נחפש מיהו
הקבועים נקבעים לפי תנאי שפה/התחלה. במקרה שלנו המיתר מוחזק בשני קצותיו, ולכן
כעת:
מספר הגל: בניגוד למקרה של הגל הרץ, בו k יכול לקבל כל ערך ממשי, במקרה
של גל עומד (במערכת סגורה), הערך של k הוא כפולה שלמה של תדירות זוויתית: תדירות יסודית של גל עומד היא
גלים בתווך תלת ממדי (מרחב) ודו ממדי (מישור) א. גל רץ במרחב 1. גלים מישוריים: במימד אחד קיבלנו: בשלושה ממדים מתקיים: פתרון של משוואת גל רץ בתווך 3 ממדי: הוכחה:
פתרון של משוואת גל רץ בתווך 2 ממדי: הגדרה חזית הגל - המקום הגאומטרי שבו
זמן נתון t יש ל- מקרה פרטי: גל מישורי הרמוני
רץ:
מהירות הפאזה:
2. גל כדורי (במישור - גל מעגלי): נובע ממקור נקודתי.
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


 . למיתר אורך L. המיתר
עשוי מחומר בצפיפות
. למיתר אורך L. המיתר
עשוי מחומר בצפיפות 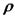 , והוא מתוח בצפיפות אורכית
, והוא מתוח בצפיפות אורכית 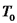 . כל נקודה מבצעת תנועה הרמונית. האמפליטודה היא
פונקציה של המקום.
. כל נקודה מבצעת תנועה הרמונית. האמפליטודה היא
פונקציה של המקום.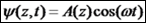 .
.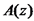 :
: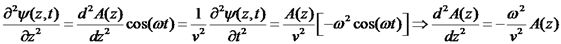
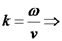
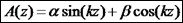
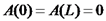 .ידוע כי
.ידוע כי 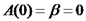 ולכן:
ולכן: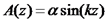 .
. 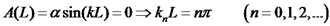
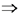
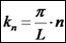 אורך
הגל:
אורך
הגל: 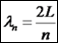
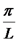 . כמו כן:
. כמו כן: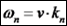 תדירות
גל עומד:
תדירות
גל עומד: 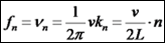
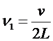 . כמו כן,
. כמו כן, 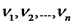 נקראות תדירויות הרמוניות של המיתר, והן מגדירות את כל
התדירויות האפשריות למיתר.
נקראות תדירויות הרמוניות של המיתר, והן מגדירות את כל
התדירויות האפשריות למיתר.

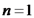 תנועה יסודית
תנועה יסודית
 הרמונית ראשונה
הרמונית ראשונה
 הרמונית שנייה
הרמונית שנייה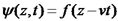 .
. 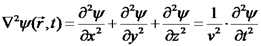
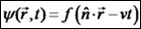
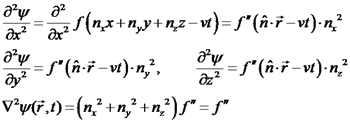
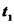 מסויים:
מסויים: 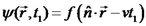 .
.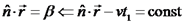 , כאשר
, כאשר 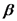 קבוע.
קבוע. 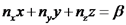 זוהי משוואה של מישור אשר ניצב ל-
זוהי משוואה של מישור אשר ניצב ל-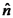 (וקטור יחידה במרחב מגדיר מישור הניצב לו).
(וקטור יחידה במרחב מגדיר מישור הניצב לו).
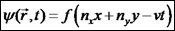
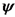 ערך מסויים. כאשר חזית הגל
היא מישורית, הגל הוא גל מישורי (3 ממדים). כאשר הגל הוא דו ממדי - חזית הגל היא
חזית קווית.
ערך מסויים. כאשר חזית הגל
היא מישורית, הגל הוא גל מישורי (3 ממדים). כאשר הגל הוא דו ממדי - חזית הגל היא
חזית קווית.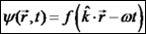
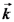 זהו ווקטור הגל
(ווקטור קבוע!). מתקיים:
זהו ווקטור הגל
(ווקטור קבוע!). מתקיים: 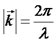 .
. 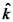 זהו כיוון התקדמות הגל.
זהו כיוון התקדמות הגל. 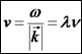
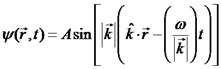
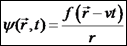
תיקון על התאבכות של N סדקים
כתבת בהערה השנייה שיש יותר מינימות מאשר מקסימות אך זה לא נכון (מכיוון שהפונקציה גזירה...), בין כל 2 מקסימות יש מינימה ובין כל 2 מינימות יש מקסימה.