5.5.2. קבוצות שאינן בנות מניה – שיטת הליכסון של קנטורתהי ניתן להציג את
(מניחים כי
הקבוצה במקום ה- דוגמא תהי
נכתוב את
כל עמודה בטבלה מגדירה תת קבוצה של מציאת העמודה השונה מכל העמודות טבלה היא העמודה המתקבלת על ידי היפוך העמודות באלכסון. כלומר, אם
באופן כללי, העמודה השונה מכל עמודה אחרת בעמודה ה- טכניקה זו שימושית – בעזרתה מוכיחים שקבוצות אינן בנות מניה. תגיות המסמך:תודה רבה!תודה על ההסבר המצויןתודהמברוק! תודהיש לכם טעותבסגור הטרנזיטיבי שהתקבל אצלכם, קיימים הזוגות <4,1> ו-<1,4>, אבל מתוקף היותו טרנזיטיבי הוא חייב גם להכיל את <1,1> ו-<4,4>. ההגדרה של טרנזיטיביות לא מחייבית a,b,c שונים.כנ"ל לגבי <2,3> ו-<4,2> - חייב להימצא הזוג הסדור <4,3>. מצאתי עוד 3 דוגמאות כאלה.. מבלבלהיית צריך לתת דוגמאות גם ליחסים לא סימטריים.... התבלבלתי ממש בין X לY בגלל זה...מבלבלהיית צריך לתת דוגמאות גם ליחסים לא סימטריים.... התבלבלתי ממש בין X לY בגלל זה...קבוצה סופיתמישו יכול להעלות את ההוכחה לכך שכל תת קבוצה של קבוצה סופית היא סופית ? זה ברור אבל אני צריך את ההגדרה הפורמלית לזה ..תודה רבהתודה רבה ספר מעולה מסביר מצויין שתצליח תמיד :-)סגור טרנזיטיביניר אתה בטוח ש- (4,2) הוא חלק מהסגור הטרנזיטיבי (משפט 3 מלמעלה)?אני לא סגור על החומר, אבל אני לא חושב שזה נכון... יפה מאוד אך ישנן כמה טעויותישנן כמה טעויות (קריטיות להוכחה) כשעברתי על החומר,למשל בהוכחה ש R* טרנזיטיבית (סעיף 2) יש בלבול שלם בין x,y,z אז צריך לתקן את זה. כל הכבוד!!!!כל הכבוד על העבודה שעשית כאן!!!נורא עוזר!!!! תודה רבה רבה רבה רבה!כל הכבוד על העלאת הסיכום המעולה הזה לטובת כולם!המון תודהוואו, חומר כל כך ברור ומסודר!עברתי על עשרות ספרים ואף אחד לא ברור וענייני כמו זה - פשוט כל הכבוד! תודה, תודה תודה! תודה רבה!!!!!!!!אף פעם לא ברור לי מה האינטרס של אנשים כמוך, להעלות חומר ממש מועיל לאינטרנט בחינם...בכל אופן, רציתי לומר: כל הכבוד ותודה רבה, הסיכומים שלך מאוד עזרו לי ואני מאוד מעריך את הזמן והמאמץ שהושקע בהם. והלוואי ויהיו רבים כמוך... |
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


![plot:\[f\]](/documentResources/164/plot_1081.png) פונקציה
פונקציה ![plot:\[f:A \to P\left( A \right)\]](/documentResources/164/plot_1082.png) . נראה כי קיימת קבוצה
. נראה כי קיימת קבוצה ![plot:\[{B_f} \in P\left( A \right)\]](/documentResources/164/plot_1083.png) שאינה מתקבלת כתמונה של אחד
מאיברי
שאינה מתקבלת כתמונה של אחד
מאיברי ![plot:\[A\]](/documentResources/164/plot_1084.png) , כלומר
, כלומר ![plot:\[{B_f} \notin f(A)\]](/documentResources/164/plot_1085.png) , ומכאן שכל פונקציה
, ומכאן שכל פונקציה ![plot:\[f:A \to P(A)\]](/documentResources/164/plot_1086.png) איננה על.
איננה על.![plot:\[f\]](/documentResources/164/plot_1087.png) בצורת הטבלה הבאה:
בצורת הטבלה הבאה:![plot:\[f\left( {{a_1}} \right)\]](/documentResources/164/plot_1088.png)
![plot:\[f\left(
{{a_2}} \right)\]](/documentResources/164/plot_1089.png)
![plot:\[f\left( {{a_3}} \right)\]](/documentResources/164/plot_1090.png)
![plot:\[f\left( {{a_4}} \right)\]](/documentResources/164/plot_1091.png)
![plot:\[{a_1}\]](/documentResources/164/plot_1092.png)
![plot:\[{a_2}\]](/documentResources/164/plot_1093.png)
![plot:\[{a_3}\]](/documentResources/164/plot_1094.png)
![plot:\[{a_4}\]](/documentResources/164/plot_1095.png)
![plot:\[A\]](/documentResources/164/plot_1096.png) בת מניה כי אחרת לא ניתן
לרשום אותה בטבלה כנ"ל).
בת מניה כי אחרת לא ניתן
לרשום אותה בטבלה כנ"ל).![plot:\[\left( {{a_1},f\left( {{a_1}} \right)} \right)\]](/documentResources/164/plot_1097.png) נרשום
נרשום ![plot:\[1\]](/documentResources/164/plot_1098.png) אם
אם ![plot:\[{a_1} \in f\left( {{a_1}} \right)\]](/documentResources/164/plot_1099.png) או
או ![plot:\[0\]](/documentResources/164/plot_1100.png) אחרת. באופן כללי: במקום ה-
אחרת. באופן כללי: במקום ה-![plot:\[\left( {{a_j},f\left( {{a_k}} \right)}
\right)\]](/documentResources/164/plot_1101.png) נרשום 1 אם
נרשום 1 אם ![plot:\[{a_j} \in f\left( {{a_k}} \right)\]](/documentResources/164/plot_1102.png) ו-0 אחרת.
ו-0 אחרת.![plot:\[A\]](/documentResources/164/plot_1103.png) הקבוצה
הקבוצה ![plot:\[A = \left\{
{{a_1},{a_2},{a_3},{a_4}} \right\}\]](/documentResources/164/plot_1104.png) ותהי
ותהי ![plot:\[f\]](/documentResources/164/plot_1105.png) שמוגדרת כך:
שמוגדרת כך:![plot:\[\begin{gathered}
f\left( {{a_1}} \right) = \phi ,
& & f\left( {{a_2}} \right) = \left\{ {{a_1},{a_3}} \right\} \hfill \\
f\left( {{a_3}} \right) = \left\{
{{a_1},{a_2},{a_3}} \right\} & f\left( {{a_4}} \right) = \phi \hfill \\
\end{gathered} \]](/documentResources/164/plot_1106.png)
![plot:\[f\]](/documentResources/164/plot_1107.png) בטבלה:
בטבלה: ![plot:\[f\left( {{a_1}} \right)\]](/documentResources/164/plot_1108.png)
![plot:\[f\left(
{{a_2}} \right)\]](/documentResources/164/plot_1109.png)
![plot:\[f\left( {{a_3}} \right)\]](/documentResources/164/plot_1110.png)
![plot:\[f\left( {{a_4}} \right)\]](/documentResources/164/plot_1111.png)
![plot:\[{a_1}\]](/documentResources/164/plot_1112.png)
![plot:\[{a_2}\]](/documentResources/164/plot_1113.png)
![plot:\[{a_3}\]](/documentResources/164/plot_1114.png)
![plot:\[{a_4}\]](/documentResources/164/plot_1115.png)
![plot:\[A\]](/documentResources/164/plot_1116.png) .
.![plot:\[{B_f} \subseteq A\]](/documentResources/164/plot_1117.png) שאיננה מתקבלת על ידי
שאיננה מתקבלת על ידי ![plot:\[f\]](/documentResources/164/plot_1118.png) שקולה למציאת עמודה שאיננה מופיעה בטבלה – נמצא עמודה שתהיה שונה מכל עמודה אחרת.
שקולה למציאת עמודה שאיננה מופיעה בטבלה – נמצא עמודה שתהיה שונה מכל עמודה אחרת.![plot:\[{a_1} \not\subset f\left( {{a_1}} \right)\]](/documentResources/164/plot_1119.png) נרשום
נרשום ![plot:\[1\]](/documentResources/164/plot_1120.png) אחרת נרשום
אחרת נרשום ![plot:\[0\]](/documentResources/164/plot_1121.png) וכך
הלאה:
וכך
הלאה:![plot:\[f\left( {{a_1}} \right)\]](/documentResources/164/plot_1122.png)
![plot:\[f\left(
{{a_2}} \right)\]](/documentResources/164/plot_1123.png)
![plot:\[f\left( {{a_3}} \right)\]](/documentResources/164/plot_1124.png)
![plot:\[f\left( {{a_4}} \right)\]](/documentResources/164/plot_1125.png)
![plot:\[{a_1}\]](/documentResources/164/plot_1126.png)
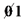
![plot:\[{a_2}\]](/documentResources/164/plot_1127.png)
![plot:\[{a_3}\]](/documentResources/164/plot_1128.png)
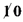
![plot:\[{a_4}\]](/documentResources/164/plot_1129.png)
![plot:\[i\]](/documentResources/164/plot_1130.png) היא שונה לפחות באיבר ה-
היא שונה לפחות באיבר ה-![plot:\[i\]](/documentResources/164/plot_1131.png) .
.![plot:[left{ {a,b}
ight}]](/documentResources/164/plot_1356.png)
![plot:[{Sigma ^*}]](/documentResources/164/plot_1372.png)
הוכחות להגדרה 2
אשמח להגדרות פורמליות מפורטות עבור המשפט. תודה רבה