4.8.2. למה 1תהי א. ב.
הוכחה א.
נתון: צ"ל: הוכחה: לפי הגדרה:
נתון: צ"ל: הוכחה: ראשית נטען כי
ולכן ב.
נתון: צ"ל: הטענה נכונה באופן טריויאלי מכיוון שגם
נתון: צ"ל: נניח בשלילה כי
כלומר ההנחה שגויה ולכן תגיות המסמך:תודה רבה!תודה על ההסבר המצויןתודהמברוק! תודהיש לכם טעותבסגור הטרנזיטיבי שהתקבל אצלכם, קיימים הזוגות <4,1> ו-<1,4>, אבל מתוקף היותו טרנזיטיבי הוא חייב גם להכיל את <1,1> ו-<4,4>. ההגדרה של טרנזיטיביות לא מחייבית a,b,c שונים.כנ"ל לגבי <2,3> ו-<4,2> - חייב להימצא הזוג הסדור <4,3>. מצאתי עוד 3 דוגמאות כאלה.. מבלבלהיית צריך לתת דוגמאות גם ליחסים לא סימטריים.... התבלבלתי ממש בין X לY בגלל זה...מבלבלהיית צריך לתת דוגמאות גם ליחסים לא סימטריים.... התבלבלתי ממש בין X לY בגלל זה...קבוצה סופיתמישו יכול להעלות את ההוכחה לכך שכל תת קבוצה של קבוצה סופית היא סופית ? זה ברור אבל אני צריך את ההגדרה הפורמלית לזה ..תודה רבהתודה רבה ספר מעולה מסביר מצויין שתצליח תמיד :-)סגור טרנזיטיביניר אתה בטוח ש- (4,2) הוא חלק מהסגור הטרנזיטיבי (משפט 3 מלמעלה)?אני לא סגור על החומר, אבל אני לא חושב שזה נכון... יפה מאוד אך ישנן כמה טעויותישנן כמה טעויות (קריטיות להוכחה) כשעברתי על החומר,למשל בהוכחה ש R* טרנזיטיבית (סעיף 2) יש בלבול שלם בין x,y,z אז צריך לתקן את זה. כל הכבוד!!!!כל הכבוד על העבודה שעשית כאן!!!נורא עוזר!!!! תודה רבה רבה רבה רבה!כל הכבוד על העלאת הסיכום המעולה הזה לטובת כולם!המון תודהוואו, חומר כל כך ברור ומסודר!עברתי על עשרות ספרים ואף אחד לא ברור וענייני כמו זה - פשוט כל הכבוד! תודה, תודה תודה! תודה רבה!!!!!!!!אף פעם לא ברור לי מה האינטרס של אנשים כמוך, להעלות חומר ממש מועיל לאינטרנט בחינם...בכל אופן, רציתי לומר: כל הכבוד ותודה רבה, הסיכומים שלך מאוד עזרו לי ואני מאוד מעריך את הזמן והמאמץ שהושקע בהם. והלוואי ויהיו רבים כמוך... |
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


![plot:\[A\]](/documentResources/164/plot_760.png) קבוצה, שני איברים
קבוצה, שני איברים ![plot:\[x,y \in A\]](/documentResources/164/plot_761.png) ותהי
ותהי ![plot:\[E\]](/documentResources/164/plot_762.png) רלצית שקילות מעל A, אזי:
רלצית שקילות מעל A, אזי:![plot:\[\left[ x \right] = \left[ y \right]\]](/documentResources/164/plot_763.png) אמ"מ
אמ"מ ![plot:\[\left\langle {x,y} \right\rangle \in E\]](/documentResources/164/plot_764.png) .
.![plot:\[[x] \ne [y]\]](/documentResources/164/plot_765.png) אמ"מ
אמ"מ ![plot:\[[x] \cap [y] = \varphi \]](/documentResources/164/plot_766.png) .
.![plot:\[\left\langle {x,y} \right\rangle \notin E\]](/documentResources/164/plot_767.png) אמ"מ
אמ"מ ![plot:\[[x] \cap [y] = \varphi \]](/documentResources/164/plot_768.png) .
.![plot:\[ \Leftarrow \]](/documentResources/164/plot_769.png)
![plot:\[\left[ x \right] = \left[ y \right]\]](/documentResources/164/plot_770.png) .
.![plot:\[\left\langle {x,y} \right\rangle \in E\]](/documentResources/164/plot_771.png) .
.![plot:\[y \in \left[ y \right]\]](/documentResources/164/plot_772.png) . נתון כי
. נתון כי ![plot:\[\left[ x \right] = \left[ y \right]\]](/documentResources/164/plot_773.png) ומכאן
ומכאן ![plot:\[y \in \left[ x \right]\]](/documentResources/164/plot_774.png)
![plot:\[ \Leftarrow \]](/documentResources/164/plot_775.png)
![plot:\[\left\langle {x,y} \right\rangle \in E\]](/documentResources/164/plot_776.png) .
.![plot:\[ \Rightarrow \]](/documentResources/164/plot_777.png)
![plot:\[\left\langle {x,y} \right\rangle \in E\]](/documentResources/164/plot_778.png)
![plot:\[\left[ x \right] = \left[ y \right]\]](/documentResources/164/plot_779.png)
![plot:\[\left\langle {y,x} \right\rangle \in
E\]](/documentResources/164/plot_780.png) (מכיוון ש-
(מכיוון ש-![plot:\[E\]](/documentResources/164/plot_781.png) הינה סימטרית). וכעת:
הינה סימטרית). וכעת: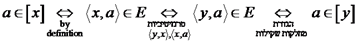
![plot:\[\left[ x \right] = \left[ y \right]\]](/documentResources/164/plot_782.png) .
.![plot:\[ \Rightarrow \]](/documentResources/164/plot_783.png)
![plot:\[[x] \cap [y] = \varphi \]](/documentResources/164/plot_784.png) .
.![plot:\[[x] \ne [y]\]](/documentResources/164/plot_785.png) .
.![plot:\[\left[ x \right]\]](/documentResources/164/plot_786.png) וגם
וגם ![plot:\[\left[ y \right]\]](/documentResources/164/plot_787.png) אינן ריקות.
אינן ריקות.![plot:\[ \Leftarrow \]](/documentResources/164/plot_788.png)
![plot:\[[x] \ne [y]\]](/documentResources/164/plot_789.png) .
.![plot:\[[x] \cap [y] = \varphi \]](/documentResources/164/plot_790.png) .
.![plot:\[[x] \cap [y] \ne \phi \]](/documentResources/164/plot_791.png) . כלומר קיים
. כלומר קיים ![plot:\[a \in \left[ x \right],\left[ y \right]\]](/documentResources/164/plot_792.png) ומכאן:
ומכאן:![plot:\[\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
\begin{gathered}
\left\langle {x,a} \right\rangle
\in E \hfill \\
\left\langle {y,a} \right\rangle
\in E \hfill \\
\end{gathered} & \Rightarrow
\\
\end{array} } \\
\end{array} \begin{array}{*{20}{c}}
\begin{gathered}
\left\langle {x,a} \right\rangle
\in E \hfill \\
\left\langle {a,y} \right\rangle
\in E \hfill \\
\end{gathered} & \Rightarrow
\\
\end{array} \left\langle {x,y}
\right\rangle \in E\mathop \Rightarrow \limits_{{\text{Lemma 1}}} \left[ x
\right] = \left[ y \right]\]](/documentResources/164/plot_793.png)
![plot:\[[x] \cap [y] = \varphi \]](/documentResources/164/plot_794.png) .
.![plot:[left{ {a,b}
ight}]](/documentResources/164/plot_1356.png)
![plot:[{Sigma ^*}]](/documentResources/164/plot_1372.png)
הוכחות להגדרה 2
אשמח להגדרות פורמליות מפורטות עבור המשפט. תודה רבה