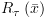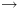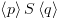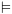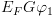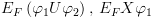6.5.6. יצוג מבנה קריפקה בעזרת BDDBDD זו דרך שימושית לייצג יחסים על פני תחום סופי. נראה
כיצד ניתן לייצג את מכונת קריפקה באמצעות BDD. שיטת העבודה בה נשתמש: נניח
ש-
אחרת תהא
כאשר מכונת קריפקה כאמור הינה כדי לייצג את הרלציה בעניין פונקצית המיפוי לכל נוסחה אטומית
אין תגובות!
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


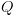 זו רלציה
זו רלציה 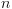 -ממדית מעל
-ממדית מעל 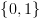 אזי
אזי 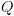 יכולה להיות מיוצגת על ידי ה-BDD עם הפונקציה האופיינית הבאה:
יכולה להיות מיוצגת על ידי ה-BDD עם הפונקציה האופיינית הבאה: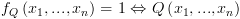
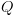 רלציה
רלציה 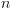 -ממדית מעל תחום סופי
-ממדית מעל תחום סופי 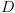 .
ללא הגבלת כלליות, נניח שב-
.
ללא הגבלת כלליות, נניח שב-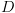 ישנם
ישנם 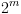 אלמנטים (
אלמנטים (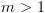 ). על מנת לייצג את
). על מנת לייצג את 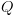 כ-BDD, נקודד את האלמנטים של
כ-BDD, נקודד את האלמנטים של 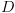 על ידי הטרנספורמציה
על ידי הטרנספורמציה ![plot:$\phi :{\left[ {0,1} \right]^m} \to D$](/documentResources/326/plot_1585.png) שממפה כל ווקטור בוליאני באורך
שממפה כל ווקטור בוליאני באורך 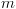 אל אלמנט ב-
אל אלמנט ב-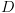 . על ידי שימוש בקידוד
. על ידי שימוש בקידוד 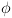 נוכל לבנות רלציה בינארית
נוכל לבנות רלציה בינארית 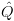 כך:
כך: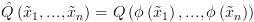
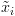 הוא ווקטור של
הוא ווקטור של 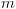 משתנים בוליאניים שמקודדים את המשתנה
משתנים בוליאניים שמקודדים את המשתנה 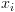 שהינו ערך מ-
שהינו ערך מ-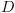 .
.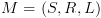 . כדי לייצג את המכונה במלואה צריכים להציג את
הקבוצה
. כדי לייצג את המכונה במלואה צריכים להציג את
הקבוצה 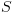 , את הרלציה
, את הרלציה 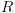 ואת פונקצית הסימון
ואת פונקצית הסימון 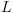 .
.
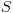 צריכים פונקציית קידוד. לצורת הנוחות נניח
צריכים פונקציית קידוד. לצורת הנוחות נניח 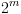 מצבים, ואז כמו עבור הרלציה נגדיר פונקצית מיפוי
בוליאנית
מצבים, ואז כמו עבור הרלציה נגדיר פונקצית מיפוי
בוליאנית ![plot:$\phi :{\left[ {0,1} \right]^m} \to S$](/documentResources/326/plot_1601.png) . ה-BDD המתאים מורכב בצורה דומה
לקודם.
. ה-BDD המתאים מורכב בצורה דומה
לקודם.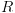 מורכבת מאותו הקידוד, כאשר אנחנו משתמשים בשני סטים מקבילים של משתנים בוליאניים
כדי להציג את המצב לפני ואת המצב לאחר המעבר
מורכבת מאותו הקידוד, כאשר אנחנו משתמשים בשני סטים מקבילים של משתנים בוליאניים
כדי להציג את המצב לפני ואת המצב לאחר המעבר 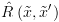 .
.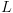 ,
למרות שהפונקציה מוגדרת בתוך מיפוי מקבוצת המצבים אל תת קבוצה של הנוסחאות
האטומיות, יותר נוח לנו להסתכל על הפונקציה כמיפוי מנוסחאות אטומיות לתת קבוצה של
מצבים. הנוסחה האטומית
,
למרות שהפונקציה מוגדרת בתוך מיפוי מקבוצת המצבים אל תת קבוצה של הנוסחאות
האטומיות, יותר נוח לנו להסתכל על הפונקציה כמיפוי מנוסחאות אטומיות לתת קבוצה של
מצבים. הנוסחה האטומית 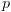 ממופה לקבוצת המצבים המספקים אותה:
ממופה לקבוצת המצבים המספקים אותה: 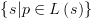 . אם נסמן קבוצה זו ב-
. אם נסמן קבוצה זו ב-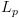 ,
נוכל להציג אותה באמצעות הקידוד
,
נוכל להציג אותה באמצעות הקידוד 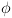 כמו שהצגנו קודם. באופן כזה, נוכל להציג כל אחד
מהביטויים האטומיים. כלומר:
כמו שהצגנו קודם. באופן כזה, נוכל להציג כל אחד
מהביטויים האטומיים. כלומר: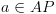 נקבל את ה-BDD שמייצג את קבוצת המצבים המספקים את
נקבל את ה-BDD שמייצג את קבוצת המצבים המספקים את 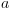 ונסמנו ב-
ונסמנו ב-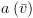 .
.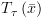 ושל
ושל