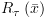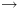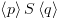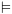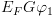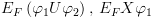5.1.4.1. אקסיומותאקסיומת ההצבה - האקסיומה הראשונה שנציג הינה אקסיומת ההצבה. אקסיומה זו מעט מסובכת להבנה בהתקלות ראשונה, ולכן נסביר אותה בפירוט. דגש ראשון: את אקסיומת ההצבה קוראים מימין לשמאל.
דוגמא 1:
נביט בחלק הימני: לחילופין, אם נתון רק הצד השמאלי: ניסוח חלופי לאקסיומת ההצבה: מדוע לא ניסחנו טענה בסגנון
אקסיומת skip - אקסיומות
אריתמטיות: כל טענה מהצורה
אין תגובות!
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


![plot:$\left\{ {p\left[ {x \leftarrow e} \right]}
\right\}x: = e\left\{ p \right\}$](/documentResources/326/plot_789.png) . (תסומן ב-ASS)
. (תסומן ב-ASS)![plot:$p\left[ {x
\leftarrow e} \right]$](/documentResources/326/plot_790.png) הוא התנאי החלש ביותר שמבטיח ש-
הוא התנאי החלש ביותר שמבטיח ש-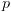 יתקיים לאחר ביצוע
יתקיים לאחר ביצוע 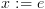 . משמעותו: לקחנו את התוכנית
. משמעותו: לקחנו את התוכנית 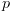 והצבנו בכל מקום במקום
והצבנו בכל מקום במקום 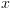 את הערך
את הערך  .
.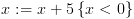 - השאלה שאנחנו שואלים הינה:
"מה צריך לדרוש כדי שיתקיים
- השאלה שאנחנו שואלים הינה:
"מה צריך לדרוש כדי שיתקיים 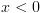 אחרי ביצוע של הפעולה
אחרי ביצוע של הפעולה 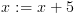 ?".
התשובה היא
?".
התשובה היא 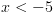 , ולכן
נכתוב:
, ולכן
נכתוב: 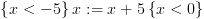 . מבחינת טכניקה: נוכל לקבל את
הצד השמאלי על ידי הצבת
. מבחינת טכניקה: נוכל לקבל את
הצד השמאלי על ידי הצבת  בכל מקום שבו מופיע
בכל מקום שבו מופיע 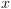 ב-
ב-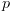 , וכך לייצר את הצד השמאלי.
, וכך לייצר את הצד השמאלי.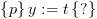 אנחנו יכולים ליצור את הצד הימני באופן
אינטואיטיבי, על ידי הפעלת הפקודה שבתוכנית על החלק השמאלי.
אנחנו יכולים ליצור את הצד הימני באופן
אינטואיטיבי, על ידי הפעלת הפקודה שבתוכנית על החלק השמאלי.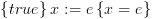 ? מכיוון שכאן אין קשר בין המצב ההתחלתי לסופי. ראו
לדוגמא:
? מכיוון שכאן אין קשר בין המצב ההתחלתי לסופי. ראו
לדוגמא: 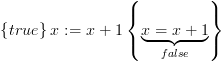 . כאשר
. כאשר  אינו תלוי ב-
אינו תלוי ב-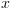 מתקיים כי
מתקיים כי 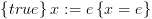 היא אקסיומה נכונה. למשל:
היא אקסיומה נכונה. למשל: 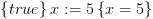
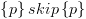 . האקסיומה תסומן
. האקסיומה תסומן 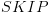 .
.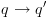 שהינה אמת לוגית הינה
אקסיומה. אקסיומות אלו יסומנו ב-
שהינה אמת לוגית הינה
אקסיומה. אקסיומות אלו יסומנו ב-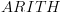 .
.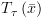 ושל
ושל