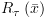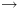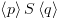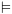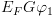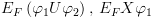5.1.4.4. משפט השלמות של Hאם זוהי שלמות יחסית. נסביר מהי שלמות יחסית ומדוע השלמות של H היא כזו. השלמות אינה מתקיימת תמיד במקרה של H, עקב מספר נושאים:
מכיוון שכך, אנו אומרים כי "אם אין
בעיות בלוגיקה מסדר ראשון בה אנו משתמשים", אז מתקיימת שלמות. לכן אנחנו לא
נדרשים להוכיח טענות לוגיקה מסדר ראשון בכלל CONS. כלומר, אנחנו עדיין צריכים
להסתכל שהטענות ב-CONS נכונות, אבל אנחנו בודקים אותן בעזרת ידע מוקדם.
לדוגמא – אנחנו מסתכלים על הטענות
אין תגובות!
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


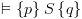 אז
אז 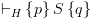
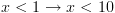 ואומרים – "הטענה נכונה (ARITH) לפי ידע קודם ממתמטיקה".
ואומרים – "הטענה נכונה (ARITH) לפי ידע קודם ממתמטיקה".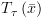 ושל
ושל