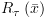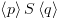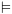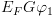5.1.2. רלציית המעברים
|
|
הגדרה: |
|
הגדרה: המשמעות
(סמנטיקה) של תוכנית S היא ![plot:$M\left[ S \right]\left( \sigma \right) = Val\left( {\pi \left( {S,\sigma }
\right)} \right)$](/documentResources/326/plot_733.png) .
.
דגש: נשים
לב כי לפי ההגדרה, חישוב של B לוקח תמיד צעד אחד 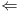 חישוב לא יכול
"להתקע" ב-B
חישוב לא יכול
"להתקע" ב-B
אין תגובות!
תוכן העניינים:
- מבוא
- לוגיקה מסדר ראשון - תקציר
- הוכחת נכונות של תוכניות
- תרשימי זרימה – Flowcharts
- הגדרות
- סמנטיקה
- למת ההפרדה
- שיטת / כללי ההוכחה
- לוגיקה של תוכניות
- אימות אוטומטי - שיטות לבדיקת מודל
- מבוא
- מבנה קריפקה - Kripke Structure
- לוגיקות טמפורליות פסוקיות
- אלגוריתם מפורש לבדיקת מודל CTL
- BDD - Binary Decision Diagram
- תיאור קבוצה ע"י פונקציה בוליאנית
- יצוג מבנה קריפקה על ידי פונקציה בוליאנית - דוגמא
- BDD - דוגמא ראשונה
- BDD כמבנה נתונים
- פעולות על BDDs:
- יצוג מבנה קריפקה בעזרת BDD
- בדיקת מודל סימבולית מבוססת BDD
- בדיקת מודל סימבולית מבוססת SAT
- תזכורת – בעיית SAT
- בדיקת מודל מבוססת SAT – Bounded Model Checking
- הוכחת נכונות בעזרת SAT – Unbounded Model Checking
- תרגילים ודוגמאות
- פתרונות לבעיית SAT – SAT Solver
- נוסחאון
- מקורות


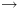
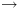 הינה הרלציה הקטנה ביותר המקיימת את ההגדרה
האינדוקטיבית הבאה:
הינה הרלציה הקטנה ביותר המקיימת את ההגדרה
האינדוקטיבית הבאה:![plot:$\left\langle {x: = e,\sigma } \right\rangle \to \left\langle {E,\sigma \left[ {x
\leftarrow \sigma \left( e \right)} \right]} \right\rangle $](/documentResources/326/plot_710.png)
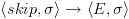
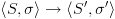 אז
אז 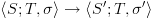 .
.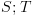 הינו חישוב של
הינו חישוב של 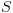 במלואו ולאחר מכן חישוב של
במלואו ולאחר מכן חישוב של 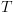 .
.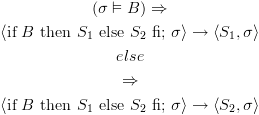
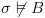 אזי
אזי 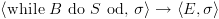 .
.![plot:\[\left\langle {{\text{while
}}B{\text{ do }}S{\text{ od, }}\sigma } \right\rangle \to \left\langle {S;{\text{while
}}B{\text{ do }}S{\text{ od}},\sigma } \right\rangle \]](/documentResources/326/plot_188.png)
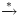 הוא הסגור הטרנזיטיבי של
הוא הסגור הטרנזיטיבי של 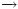 . אם נכתוב
. אם נכתוב 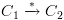 המשמעות היא שניתן לעבור מ-
המשמעות היא שניתן לעבור מ-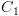 ע"י מספר סופי של צעדים
(כולל 0) ל-
ע"י מספר סופי של צעדים
(כולל 0) ל-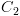 .
.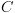 המסומן
המסומן 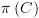 הינו סדרה מקסימלית של
קונפיגורציות
הינו סדרה מקסימלית של
קונפיגורציות 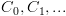 כך ש-
כך ש-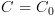 ולכל
ולכל  מתקיים
מתקיים 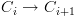 .
.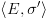 - קונפיגורציה עוצרת.
- קונפיגורציה עוצרת.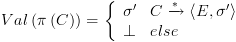
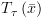 ושל
ושל