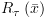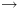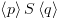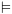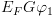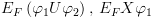5.1.4.3. משפט הנאותות של Hמשפט: אם ההוכחה תהיה באינדוקציה על מבנה ההוכחה ב-H. נראה שכל אחת מהאקסיומות תמיד נכונה. נראה כי לכל כלל היסק, אם מתקיים החלק העליון שבכלל, אזי מתקיים גם החלק התחתון. בסיס
אם החישוב התחיל במצב לפי למת החישובים, החישוב היחיד שיש להשמה הוא החישוב הבא:
צריך להוכיח כי כעת נבדוק עבור נשתמש שוב בלמת החישובים, ונראה כי צריך
להוכיח: הוכחת כללי ההיסק הרכבה סדרתית (SEQ): נתון: צ"ל: נשאל את עצמנו איזה סוג חישובים יש
להרכבה סידרתית לפי למת החישובים. ישנם חישובים מתבדרים וישנם חישובים עוצרים. המקרה
בו אנו מתעניינים עבור נכונות חלקית הוא מקרה שבו גם החלק עפ"י הנתון:
מ- לולאה (REP): נתון: צ"ל: למת החישובים: מעניין אותנו לבדוק חישובים שעוצרים, כי עבור חישובים שלא עוצרים הטענה נכונה באופן טריויאלי.
באינדוקציה על מספר ביצועי החוג, נראה
כי לכל בסיס: צ"ל כי צעד: נניח כי על פי עבור כלל CONS: נתון: צריך להוכיח: יהי על סמך נתון 2: על סמך נתון 3: על סמך טרנזיטיביות הגזירה נקבל: כלל COND: הכלל מוכח באופן דומה ל-SEQ. ההוכחה לא תוצג במסמך זה.
אין תגובות!
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


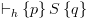 אז
אז 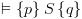
![plot:$
\vDash \left\{ {p\left[ {x \leqslant e} \right]} \right\}x: = e\left\{ p
\right\}$](/documentResources/326/plot_847.png)
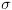 כך
שמתקיים
כך
שמתקיים ![plot:$\sigma
\vDash p\left[ {x \leftarrow e} \right]$](/documentResources/326/plot_849.png) אז המצב הסופי
אז המצב הסופי 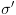 יספק את
יספק את 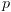 .
.![plot:$\left\langle
{x: = e,\sigma } \right\rangle \to
\left\langle {E,\sigma \left[ {x \leftarrow e} \right]} \right\rangle $](/documentResources/326/plot_852.png)
![plot:$\sigma \vDash p\left[ {x \leftarrow e} \right] \to
\sigma \left[ {x \leftarrow e} \right] \vDash p$](/documentResources/326/plot_853.png) . ביטוי זה נכון לפי המשפט מלוגיקה.
. ביטוי זה נכון לפי המשפט מלוגיקה.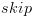 :
: 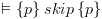
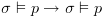 , ביטוי שהוא נכון.
, ביטוי שהוא נכון.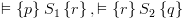
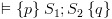
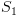 וגם
וגם 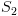 עוצרים. עפ"י למת החישובים מתקיים
עוצרים. עפ"י למת החישובים מתקיים 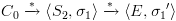 .
.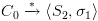 מתאים לחישוב סופי של
מתאים לחישוב סופי של 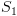 מלבד תוספת
מלבד תוספת 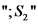 בכל
קונפיגורציה.
בכל
קונפיגורציה.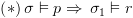
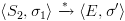 הוא חישוב של
הוא חישוב של 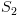 ולכן עפ"י הנתון:
ולכן עפ"י הנתון: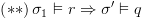
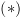 ומ-
ומ-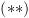 נסיק ש-
נסיק ש- 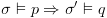 כנדרש.
כנדרש.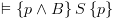
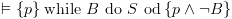
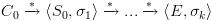 . נסמן ב-
. נסמן ב-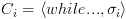 . אנו יודעים כי עבור
. אנו יודעים כי עבור 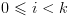 מתקיים
מתקיים
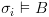 וכן כי
וכן כי 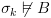 .
. מתקיים
מתקיים 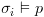 ,
בתנאי ש-
,
בתנאי ש-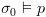 .
.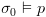 .
זה נכון מכיוון שזה נתון.
.
זה נכון מכיוון שזה נתון.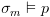 .
נראה כי
.
נראה כי 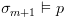 עבור
עבור 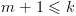 .
.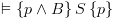 אז לכל
אז לכל 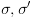 כך שהחישוב של
כך שהחישוב של 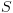 מתחיל ב-
מתחיל ב-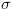 ומסתיים
ב-
ומסתיים
ב-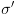 מתקיים
מתקיים 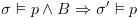 . מכאן
המסקנה
. מכאן
המסקנה 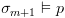 .
.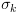 , מתקיים כי
, מתקיים כי 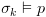 על פי ההוכחה באינדוקציה.
על פי ההוכחה באינדוקציה. 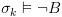 ולכן קיבלנו את מה שצריך להוכיח.
ולכן קיבלנו את מה שצריך להוכיח.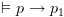
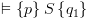
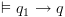
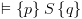
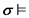 .
על סמך נתון 1, מתקיים כי
.
על סמך נתון 1, מתקיים כי 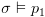 (כל מה שמספק
(כל מה שמספק 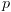 מספק את
מספק את 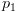 ).
).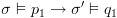
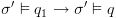
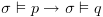 ומכאן:
ומכאן: 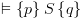
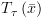 ושל
ושל