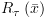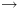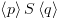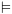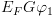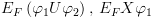2.1. תזכורת – תחשיב היחסים
הסימנים של תחשיב היחסים
הסימנים מתחלקים ל-2 קבוצות:
- סימנים לוגיים – סימנים המשותפים לכל השפות של תחשיב היחסים.
- פרמטרים של השפה – מילון – סימנים המיוחדים לשפה.
הסימנים הלוגיים
- כמתים: לכל
![plot:\[\forall \]](/documentResources/326/plot_1.png) , קיים
, קיים ![plot:\[\exists \]](/documentResources/326/plot_2.png) .
.
- קשרים של תחשיב הפסוקים:
![plot:\[\left\{ { \to , \wedge , \vee ,\neg
} \right\}\]](/documentResources/326/plot_3.png) .
.
- סוגריים ופסיק.
- סימן שוויון
![plot:\[ \approx \]](/documentResources/326/plot_4.png) .
.
- משתנים:
![plot:\[\left\{ {{v_i}|i \in \mathbb{N}}
\right\}\]](/documentResources/326/plot_5.png) .
.
מילון: פרמטרים של השפה
- סימני קבועים אישיים מסומנים ב-
![plot:\[{C_\alpha }\]](/documentResources/326/plot_6.png) כאשר
כאשר ![plot:\[\alpha \]](/documentResources/326/plot_7.png) אינדקס מספרי.
אינדקס מספרי.
- סימני יחס המסומנים ב-
![plot:\[{R_{n,\alpha }}\]](/documentResources/326/plot_8.png) כאשר
כאשר ![plot:\[n,\alpha \in \mathbb{N}\]](/documentResources/326/plot_9.png) .
. ![plot:\[n\]](/documentResources/326/plot_10.png) הוא מספר הארגומנטים ביחס ו-
הוא מספר הארגומנטים ביחס ו-![plot:\[\alpha \]](/documentResources/326/plot_11.png) הוא אינדקס מספרי.
הוא אינדקס מספרי.
- סימני פונקציה המסומנים ב-
![plot:\[{F_{n,\alpha }}\]](/documentResources/326/plot_12.png) .
. ![plot:\[n\]](/documentResources/326/plot_13.png) הוא מספר הארגומנטים ביחס ו-
הוא מספר הארגומנטים ביחס ו-![plot:\[\alpha \]](/documentResources/326/plot_14.png) הוא אינדקס מספרי.
הוא אינדקס מספרי.
מילון:
אוסף סימני יחס, סימני פונקציה וסימני קבועים אישיים, כאשר לכל סימן פונקציה ולכל
סימן יחס ידוע מספר הארגומנטים. מילון מסומן לרוב באות ![plot:\[\tau \]](/documentResources/326/plot_15.png) .
לדוגמא:
.
לדוגמא: ![plot:\[{\tau _0} = \left\langle
{{R_{1,0}},{R_{1,1}},{F_{2,0}},{F_{2,3}},{C_2},{C_3}} \right\rangle \]](/documentResources/326/plot_16.png) .
.
מילון סופי
הוא מילון המכיל מספר סופי של סימנים. מילון יחסי הוא מילון המכיל רק סימני
יחס.
הגדרת אוסף הטענות בשפה
|
שלב 1: |
הגדרת אוסף העצמים עליהם מדברים. שמות
עצם אינם טענות שניתן לשאול עליהם
נכון / לא נכון. |
|
שלב 2: |
נגדיר את אוסף הטענות בשפה שתיקראנה נוסחאות
על סמך שמות העצם. |
הגדרת אוסף שמות העצם
ההגדרה הינה באינדוקציה: (סימני פיסוק, משתנים![plot:\[ \cup \]](/documentResources/326/plot_17.png) קבועים)X.
קבועים)X.
קבוצת האטומים: סימני הקבועים מהמילון בתוספת המשתנים ![plot:\[\left\{ {{v_i}|i \in \mathbb{N}}
\right\}\]](/documentResources/326/plot_18.png) .
.
קבוצת הפעולות: לכל סימן פונקציה ![plot:\[{F_{n,\alpha }}\]](/documentResources/326/plot_19.png) במילון נגדיר פעולה המקבלת
שמות עצם
במילון נגדיר פעולה המקבלת
שמות עצם ![plot:\[{t_1},...,{t_n}\]](/documentResources/326/plot_20.png) ומוציאה כפלט את
ומוציאה כפלט את ![plot:\[{F_{n,\alpha }}\left( {{t_1},...,{t_n}} \right)\]](/documentResources/326/plot_21.png) .
.
הערה: מספר
הפעולות הינו כמספר הפונקציות במילון של השפה. ישנן שפות ללא פונקציות, ולכן ללא
פעולות ליצירת שמות עצם. מספר שמות העצם בשפות אלו זה למספר האטומים.
הגדרת אוסף הטענות/נוסחאות.
ההגדרה הינה באינדוקציה. קבוצת האטומים
הינה אוסף סדרות הסימנים מהצורה ![plot:\[{R_{n,\alpha }}\left( {{t_1},...,{t_n}}
\right)\]](/documentResources/326/plot_22.png) כאשר
כאשר ![plot:\[{t_1},...,{t_n}\]](/documentResources/326/plot_23.png) שמות עצם, ו-
שמות עצם, ו-![plot:\[{R_{n,\alpha }}\]](/documentResources/326/plot_24.png) הינו סימן יחס
הינו סימן יחס ![plot:\[n\]](/documentResources/326/plot_25.png) -מקומי מהמילון. כל סדרת סימנים כזו תקרא נוסחה
אטומית.
-מקומי מהמילון. כל סדרת סימנים כזו תקרא נוסחה
אטומית.
אבחנה: בשם עצם יכולות להיות כלולות כמה
פונקציות. בנוסחה אטומית יש רק סימן יחס אחד (ואחד או יותר שמות עצם).
עבור הגדרת אוסף הנוסחאות נתייחס לסימן
"=" כאל סימן יחס דו מקומי. דוגמא: ![plot:\[F\left( {x,x} \right) = F\left( {x,y}
\right)\]](/documentResources/326/plot_26.png) זוהי נוסחה אטומית.
זוהי נוסחה אטומית.
קבוצת אוסף הפעולות מתחלקת לשני חלקים:
- הפעלת הקשרים של תחשיב הפסוקים. אם
![plot:\[\alpha ,\beta \]](/documentResources/326/plot_27.png) נוסחאות, אזי גם
הביטויים הנ"ל הם נוסחאות:
נוסחאות, אזי גם
הביטויים הנ"ל הם נוסחאות: ![plot:\[\left( {\alpha \wedge \beta } \right),\left(
{\alpha \vee \beta } \right),\left(
{\alpha \to \beta } \right),\left(
{\neg \alpha } \right)\]](/documentResources/326/plot_28.png) .
.
- הפעלת כמתים: לכל נוסחה
![plot:\[\alpha \]](/documentResources/326/plot_29.png) ומשתנה
ומשתנה ![plot:\[x\]](/documentResources/326/plot_30.png) ,
גם
,
גם ![plot:\[\forall x\alpha \]](/documentResources/326/plot_31.png) ו-
ו-![plot:\[\exists x\alpha \]](/documentResources/326/plot_32.png) הן נוסחאות.
הן נוסחאות.
הערה: מניחים קדימות לכמתים: ![plot:\[\forall {v_i}P\left( {{v_i}} \right) \to R\left( {{v_r}} \right) \equiv
\left( {\forall {v_i}P\left( {{v_i}} \right)} \right) \to R\left( {{v_r}}
\right)\]](/documentResources/326/plot_33.png)
הבדלים בין סימני יחס לפונקציות
![plot:\[F\left( {F\left( {} \right)} \right)\]](/documentResources/326/plot_34.png) הינו שם עצם.
הינו שם עצם. ![plot:\[R\left( {R\left( {} \right)} \right)\]](/documentResources/326/plot_35.png) לא מוגדר כחלק מתחשיב היחסים!
לא מוגדר כחלק מתחשיב היחסים!
![plot:\[R\left( {F\left( {} \right)} \right)\]](/documentResources/326/plot_36.png) הינה נוסחה אטומית.
הינה נוסחה אטומית. ![plot:\[F\left( {R\left( {} \right)} \right)\]](/documentResources/326/plot_37.png) לא קיים – אסור להפעיל סימני פונקציה על יחס.
לא קיים – אסור להפעיל סימני פונקציה על יחס.
![plot:\[R \to R\]](/documentResources/326/plot_38.png) מותר.
מותר. ![plot:\[F \to F\]](/documentResources/326/plot_39.png) - אסור. יש לתת סימני יחס בין הקשרים והכמתים.
- אסור. יש לתת סימני יחס בין הקשרים והכמתים.
![plot:\[\forall xR\]](/documentResources/326/plot_40.png) מותר.
מותר. ![plot:\[\forall xF\]](/documentResources/326/plot_41.png) אסור.
אסור.
סמנטיקה לתחשיב היחסים - הגדרה
אינטואיטיבית
בהינתן מילון ![plot:\[\tau \]](/documentResources/326/plot_42.png) ,
,
![plot:\[\tau
= \left\langle {{R_1},...,{R_m},{F_1},...,{F_k},{C_1}...,{C_l}}
\right\rangle \]](/documentResources/326/plot_43.png) מבנה עבור
מבנה עבור ![plot:\[\tau \]](/documentResources/326/plot_44.png) מוגדר כך:
מוגדר כך:
![plot:\[M
= \left\langle {{D^M},{R_1}^M,...,{R_m}^M,{F^M}_1,...,{F_k}^M,{C_1}^M...,{C_l}^M}
\right\rangle \]](/documentResources/326/plot_45.png)
כאשר ![plot:\[{D^M}\]](/documentResources/326/plot_46.png) הוא התחום,
הוא התחום, ![plot:\[{R_i}^M\]](/documentResources/326/plot_47.png) הוא הפירוש של סימן היחס
הוא הפירוש של סימן היחס ![plot:\[{R_i}\]](/documentResources/326/plot_48.png) במבנה
במבנה ![plot:\[M\]](/documentResources/326/plot_49.png) ,
, ![plot:\[{F_i}^M\]](/documentResources/326/plot_50.png) הוא הפירוש של סימן הפונקציה
הוא הפירוש של סימן הפונקציה ![plot:\[{F_i}\]](/documentResources/326/plot_51.png) במבנה
במבנה ![plot:\[M\]](/documentResources/326/plot_52.png) ,
, ![plot:\[{C_i}^M\]](/documentResources/326/plot_53.png) הוא הפירוש של סימן הקבוע
הוא הפירוש של סימן הקבוע ![plot:\[{C_i}\]](/documentResources/326/plot_54.png) במבנה
במבנה ![plot:\[M\]](/documentResources/326/plot_55.png) .
.
דוגמא: ![plot:\[\tau = \left\langle
{{R_{2,0}},{F_{1,0}},{C_0},{C_1}} \right\rangle \]](/documentResources/326/plot_56.png) .
. ![plot:\[{M_2} = \left\langle {P\left( A \right),
\subseteq ,{\text{completion}},\phi ,A} \right\rangle ,{M_1} = \left\langle
{\mathbb{N}, \leqslant , + 1,2,3} \right\rangle \]](/documentResources/326/plot_57.png) .
.
בהינתן מבנה עבור מילון ![plot:\[\tau \]](/documentResources/326/plot_58.png) ,
נגדיר השמה
,
נגדיר השמה ![plot:\[z\]](/documentResources/326/plot_59.png) המתאימה למשתנים ערכים מהתחום:
המתאימה למשתנים ערכים מהתחום:
![plot:\[z:\left\{
{{v_i}|i \in \mathbb{N}} \right\} \to {D^M}\]](/documentResources/326/plot_60.png)
נגדיר הרחבה של ההשמה ![plot:\[z\]](/documentResources/326/plot_61.png) ,
שתתאים לכל שם עצם
,
שתתאים לכל שם עצם ![plot:\[t\]](/documentResources/326/plot_62.png) מעל המילון
מעל המילון ![plot:\[\tau \]](/documentResources/326/plot_63.png) איבר בתחום שיסומן
איבר בתחום שיסומן ![plot:\[\bar z\left( t \right)\]](/documentResources/326/plot_64.png) .
.
נגדיר באינדוקציה על מבנה שמות העצם:
בסיס: ![plot:\[t\]](/documentResources/326/plot_65.png) משתנה
משתנה![plot:\[\bar z\left( t \right) = z\left( t
\right) \Leftarrow \]](/documentResources/326/plot_66.png) .
. ![plot:\[t\]](/documentResources/326/plot_67.png) קבוע
קבוע![plot:\[\bar z\left( {{c_i}} \right) = {c_i}^M
\Leftarrow t = {c_i} \Leftarrow \]](/documentResources/326/plot_68.png) .
.
סגור: ![plot:\[\bar z\left( {{F_{n,\alpha }}\left(
{{t_1},...,{t_n}} \right)} \right) = F_{n,\alpha }^M\left( {\bar z\left(
{{t_1}} \right),...,\bar z\left( {{t_n}} \right)} \right)\]](/documentResources/326/plot_69.png) .
.
משתנים חופשיים וקשורים
![plot:\[\forall {v_1}{R_{2,0}}\left(
{{v_1},{v_1}} \right)\]](/documentResources/326/plot_70.png) - כל האיברים בתחום הם ביחס עם עצמם.
- כל האיברים בתחום הם ביחס עם עצמם.![plot:\[{R_{2,0}}\left( {{v_1},{v_1}} \right)\]](/documentResources/326/plot_71.png) -
- ![plot:\[{v_1}\]](/documentResources/326/plot_72.png) ביחס
ביחס ![plot:\[{R_{2,0}}\]](/documentResources/326/plot_73.png) עם עצמו.
עם עצמו.
בדוגמא הראשונה אין צורך לדעת מה הערך
של ![plot:\[{v_1}\]](/documentResources/326/plot_74.png) בהשמה, ובנוסחה השניה כן. בנוסחה הראשונה
בהשמה, ובנוסחה השניה כן. בנוסחה הראשונה ![plot:\[{v_1}\]](/documentResources/326/plot_75.png) מופיע קשור (תחת השפעת הכמת), לכן הוא אינו מופיע בתרגום הנוסחה למילים ואין צורך
לדעת את הערך שההשמה נתנה לו. בנוסחה השניה
מופיע קשור (תחת השפעת הכמת), לכן הוא אינו מופיע בתרגום הנוסחה למילים ואין צורך
לדעת את הערך שההשמה נתנה לו. בנוסחה השניה ![plot:\[{v_1}\]](/documentResources/326/plot_76.png) חופשי.
חופשי.
טענה: תהי ![plot:\[\alpha \]](/documentResources/326/plot_77.png) נוסחה מעל מילון
נוסחה מעל מילון ![plot:\[\tau \]](/documentResources/326/plot_78.png) ו-
ו-![plot:\[M\]](/documentResources/326/plot_79.png) מבנה עבור
מבנה עבור ![plot:\[\tau \]](/documentResources/326/plot_80.png) . אם
. אם ![plot:\[{z_1}\]](/documentResources/326/plot_81.png) ו-
ו-![plot:\[{z_2}\]](/documentResources/326/plot_82.png) השמות ב-
השמות ב-![plot:\[M\]](/documentResources/326/plot_83.png) המזדהות על המשתנים החופשיים ב-
המזדהות על המשתנים החופשיים ב-![plot:\[\alpha \]](/documentResources/326/plot_84.png) ,
אז ערך האמת של
,
אז ערך האמת של ![plot:\[\alpha \]](/documentResources/326/plot_85.png) תחת
תחת ![plot:\[{z_1}\]](/documentResources/326/plot_86.png) ותחת
ותחת![plot:\[{z_2}\]](/documentResources/326/plot_87.png) זהה.
זהה.
מסקנה: אם ![plot:\[\alpha \]](/documentResources/326/plot_88.png) נוסחה ללא משתנים חופשיים, אז ערך האמת של
נוסחה ללא משתנים חופשיים, אז ערך האמת של ![plot:\[\alpha \]](/documentResources/326/plot_89.png) אינו תלוי בהשמה.
אינו תלוי בהשמה.
הגדרה:
נוסחה ![plot:\[\alpha \]](/documentResources/326/plot_90.png) בלי משתנים חופשיים נקראת פסוק.
בלי משתנים חופשיים נקראת פסוק.
הגדרה פורמלית: נגדיר באינדוקציה על מבנה הנוסחה ![plot:\[\alpha \]](/documentResources/326/plot_91.png) מתי
מתי ![plot:\[{v_i}\]](/documentResources/326/plot_92.png) הוא משתנה חופשי ב-
הוא משתנה חופשי ב-![plot:\[\alpha \]](/documentResources/326/plot_93.png) .
.
בסיס: נוסחאות אטומיות: ![plot:\[{v_i}\]](/documentResources/326/plot_94.png) חופשי ב-
חופשי ב-![plot:\[\alpha \]](/documentResources/326/plot_95.png) אם
אם ![plot:\[{v_i}\]](/documentResources/326/plot_96.png) מופיע ב-
מופיע ב-![plot:\[\alpha \]](/documentResources/326/plot_97.png) .
.
סגור: קשרים:
עבור ![plot:\[ \circ
\in \left\{ { \wedge , \vee , \to } \right\}\]](/documentResources/326/plot_98.png) ,
, ![plot:\[{v_i}\]](/documentResources/326/plot_99.png) חופשי ב-
חופשי ב-![plot:\[\left( {\alpha \circ \beta } \right)\]](/documentResources/326/plot_100.png) אם
אם ![plot:\[{v_i}\]](/documentResources/326/plot_101.png) חופשי ב-
חופשי ב-![plot:\[\alpha \]](/documentResources/326/plot_102.png) או
או ![plot:\[{v_i}\]](/documentResources/326/plot_103.png) חופשי ב-
חופשי ב-![plot:\[\beta \]](/documentResources/326/plot_104.png) .
.
![plot:\[{v_i}\]](/documentResources/326/plot_105.png) חופשי ב-
חופשי ב-![plot:\[\left( {\neg \alpha } \right)\]](/documentResources/326/plot_106.png) אם
אם ![plot:\[{v_i}\]](/documentResources/326/plot_107.png) חופשי ב-
חופשי ב-![plot:\[\alpha \]](/documentResources/326/plot_108.png) .
.
כמתים: ![plot:\[{v_i}\]](/documentResources/326/plot_109.png) חופשי ב-
חופשי ב-![plot:\[\forall {v_j}\alpha \]](/documentResources/326/plot_110.png) או ב-
או ב-![plot:\[\exists {v_j}\alpha \]](/documentResources/326/plot_111.png) אם
אם ![plot:\[{v_i}\]](/documentResources/326/plot_112.png) חופשי ב-
חופשי ב-![plot:\[\alpha \]](/documentResources/326/plot_113.png) וגם
וגם ![plot:\[i \ne j\]](/documentResources/326/plot_114.png) .
.
משתנה שאינו חופשי נקרא משתנה קשור.
סמנטיקה לתחשיב היחסים - הגדרה
פורמלית
הגדרת מבנה:
בהינתן מילון ![plot:\[\tau \]](/documentResources/326/plot_115.png) :
: ![plot:\[\tau
= \left\langle {{R_1},...,{R_m},{F_1},...,{F_k},{C_1},...,{C_l}}
\right\rangle \]](/documentResources/326/plot_116.png) מבנה עבור
מבנה עבור ![plot:\[\tau \]](/documentResources/326/plot_117.png) הוא:
הוא:
![plot:\[M
= \left\langle
{{D^M},{R_1}^M,...,{R_m}^M,{F^M}_1,...,{F_k}^M,{C_1}^M...,{C_l}^M}
\right\rangle \]](/documentResources/326/plot_118.png)
כאשר ![plot:\[{D^M}\]](/documentResources/326/plot_119.png) הוא התחום.
הוא התחום.
- לכל
![plot:\[1 \leqslant i \leqslant m\]](/documentResources/326/plot_120.png) אם
אם ![plot:\[{R_i}\]](/documentResources/326/plot_121.png) הוא סימן יחס
הוא סימן יחס ![plot:\[n\]](/documentResources/326/plot_122.png) -מקומי
אזי
-מקומי
אזי ![plot:\[R_i^M \subseteq \underbrace {{D^M}
\times ... \times {D^M}}_{n{\text{ times}}}\]](/documentResources/326/plot_123.png) , כלומר
, כלומר ![plot:\[R_i^M\]](/documentResources/326/plot_124.png) הוא יחס
הוא יחס ![plot:\[n\]](/documentResources/326/plot_125.png) -מקומי
מעל
-מקומי
מעל ![plot:\[{D^M}\]](/documentResources/326/plot_126.png) .
.
- לכל
![plot:\[1 \leqslant i \leqslant k\]](/documentResources/326/plot_127.png) אם
אם ![plot:\[{F_i}\]](/documentResources/326/plot_128.png) סימן פונקציה
סימן פונקציה ![plot:\[n\]](/documentResources/326/plot_129.png) -מקומי
אז
-מקומי
אז ![plot:\[F_i^M:\underbrace {{D^M} \times
... \times {D^M}}_{n{\text{ times}}} \to {D^M}\]](/documentResources/326/plot_130.png) , כלומר
, כלומר ![plot:\[F_i^M\]](/documentResources/326/plot_131.png) מתארת מה הערך של
מתארת מה הערך של ![plot:\[{F_i}\]](/documentResources/326/plot_132.png) עבור כל
עבור כל ![plot:\[n\]](/documentResources/326/plot_133.png) -יה סדורה של איברים מ-
-יה סדורה של איברים מ-![plot:\[{D^M}\]](/documentResources/326/plot_134.png) .
.
- לכל
![plot:\[1 \leqslant i \leqslant l\]](/documentResources/326/plot_135.png) , מתקיים:
, מתקיים: ![plot:\[C_i^M \in {D^M}\]](/documentResources/326/plot_136.png) .
.
ראינו כיצד בהינתן מבנה M
מגדירים השמה ![plot:\[z\]](/documentResources/326/plot_137.png) ב-
ב-![plot:\[M\]](/documentResources/326/plot_138.png) :
: ![plot:\[z:\left\{ {{v_i}|i \in \mathbb{N}}
\right\} \to {D^M}\]](/documentResources/326/plot_139.png) וראינו כיצד להרחיב את
וראינו כיצד להרחיב את ![plot:\[z\]](/documentResources/326/plot_140.png) כך שתתאים ערך מהתחום לכל שם עצם.
כך שתתאים ערך מהתחום לכל שם עצם.
בהינתן נוסחה ![plot:\[\alpha \]](/documentResources/326/plot_141.png) מעל מילון
מעל מילון ![plot:\[\tau \]](/documentResources/326/plot_142.png) , מבנה
, מבנה ![plot:\[M\]](/documentResources/326/plot_143.png) והשמה
והשמה ![plot:\[z\]](/documentResources/326/plot_144.png) עבור
עבור ![plot:\[M\]](/documentResources/326/plot_145.png) נסמן
נסמן ![plot:\[M\mathop \vDash \limits_z \alpha \]](/documentResources/326/plot_146.png) את הטענה ש-
את הטענה ש-![plot:\[\alpha \]](/documentResources/326/plot_147.png) מסתפקת ב-
מסתפקת ב-![plot:\[M\]](/documentResources/326/plot_148.png) תחת
תחת ![plot:\[z\]](/documentResources/326/plot_149.png) .
.
הגדרת ערך האמת: נגדיר באינדוקציה על מבנה ![plot:\[\alpha \]](/documentResources/326/plot_150.png) מתי
מתי ![plot:\[M\mathop \vDash \limits_z \alpha \]](/documentResources/326/plot_151.png) .
.
בסיס: ![plot:\[\alpha \]](/documentResources/326/plot_152.png) נוסחה אטומית:
נוסחה אטומית: ![plot:\[\alpha
= \left( {{t_1} \approx {t_2}} \right)\]](/documentResources/326/plot_153.png) עבור
עבור ![plot:\[{t_1},{t_2}\]](/documentResources/326/plot_154.png) שמות עצם,
שמות עצם, ![plot:\[M\mathop \vDash \limits_z
\alpha \Leftrightarrow \bar z\left( {{t_1}}
\right) = \bar z\left( {{t_2}} \right)\]](/documentResources/326/plot_155.png) .
.
כמו כן כאשר ![plot:\[\alpha = R\left(
{{t_1},...,{t_n}} \right)\]](/documentResources/326/plot_156.png) , עבור
, עבור ![plot:\[{t_1},...,{t_n}\]](/documentResources/326/plot_157.png) שמות עצם,
שמות עצם, ![plot:\[M\mathop \vDash \limits_z
\alpha \Leftrightarrow \left( {\bar
z\left( {{t_1}} \right),...,\bar z\left( {{t_n}} \right)} \right) \in {R^M}\]](/documentResources/326/plot_158.png) .
.
סגור:
- קשרים: מחשבים את ערך האמת בעזר טבלאות האמת. לכל נוסחה
![plot:\[\alpha \]](/documentResources/326/plot_159.png) , מבנה
, מבנה ![plot:\[M\]](/documentResources/326/plot_160.png) והשמה
והשמה ![plot:\[z\]](/documentResources/326/plot_161.png) , מתקיים כי
, מתקיים כי ![plot:\[M\mathop \vDash \limits_z \alpha \]](/documentResources/326/plot_162.png) או
או ![plot:\[M\mathop \vDash \limits_z
\neg \alpha \]](/documentResources/326/plot_163.png) אבל לא שניהם.
אבל לא שניהם.
- כמתים: נניח שלכל מבנה
![plot:\[M'\]](/documentResources/326/plot_164.png) והשמה
והשמה ![plot:\[z'\]](/documentResources/326/plot_165.png) אנו יודעים האם
אנו יודעים האם ![plot:\[M'\mathop \vDash
\limits_{z'} \alpha \]](/documentResources/326/plot_166.png) . נרצה לדעת האם
. נרצה לדעת האם ![plot:\[M\mathop \vDash \limits_z \forall {v_i}\alpha \]](/documentResources/326/plot_167.png) ,
, ![plot:\[M\mathop \vDash \limits_z
\exists {v_i}\alpha \]](/documentResources/326/plot_168.png) למבנה והשמה מסויימים. בהינתן השמה
למבנה והשמה מסויימים. בהינתן השמה ![plot:\[z\]](/documentResources/326/plot_169.png) ,
משתנה
,
משתנה ![plot:\[{v_i}\]](/documentResources/326/plot_170.png) ואיבר
ואיבר ![plot:\[d \in {D^M}\]](/documentResources/326/plot_171.png) , נגדיר השמה מתוקנת
, נגדיר השמה מתוקנת ![plot:\[z\left[ {{v_i} \leftarrow d} \right]\]](/documentResources/326/plot_172.png) :
:
![plot:\[z\left[ {{v_i} \leftarrow d}
\right]\left( {{v_j}} \right) = \left\{ {\begin{array}{*{20}{c}}
{z\left( {{v_j}} \right)} \hfill & {i \ne j} \hfill \\
d \hfill & {i = j} \hfill \\
\end{array} } \right.\]](/documentResources/326/plot_173.png)
נגדיר: לכל ![plot:\[d \in {D^M}\]](/documentResources/326/plot_174.png) מתקיים
מתקיים ![plot:\[M\mathop \vDash \limits_z \forall {v_i}\alpha \Leftrightarrow M\mathop \vDash \limits_{z\left[ {{v_i} \leftarrow d}
\right]} \alpha \]](/documentResources/326/plot_175.png) .
.
קיים ![plot:\[d \in {D^M}\]](/documentResources/326/plot_176.png) עבורו
עבורו ![plot:\[M\mathop \vDash \limits_z \exists {v_i}\alpha \Leftrightarrow M\mathop \vDash \limits_{z\left[ {{v_i} \leftarrow d}
\right]} \alpha \]](/documentResources/326/plot_177.png) .
.


![plot:\[\forall \]](/documentResources/326/plot_1.png) , קיים
, קיים ![plot:\[\exists \]](/documentResources/326/plot_2.png) .
.![plot:\[\left\{ { \to , \wedge , \vee ,\neg
} \right\}\]](/documentResources/326/plot_3.png) .
.![plot:\[ \approx \]](/documentResources/326/plot_4.png) .
.![plot:\[\left\{ {{v_i}|i \in \mathbb{N}}
\right\}\]](/documentResources/326/plot_5.png) .
.![plot:\[{C_\alpha }\]](/documentResources/326/plot_6.png) כאשר
כאשר ![plot:\[\alpha \]](/documentResources/326/plot_7.png) אינדקס מספרי.
אינדקס מספרי.![plot:\[{R_{n,\alpha }}\]](/documentResources/326/plot_8.png) כאשר
כאשר ![plot:\[n,\alpha \in \mathbb{N}\]](/documentResources/326/plot_9.png) .
. ![plot:\[n\]](/documentResources/326/plot_10.png) הוא מספר הארגומנטים ביחס ו-
הוא מספר הארגומנטים ביחס ו-![plot:\[\alpha \]](/documentResources/326/plot_11.png) הוא אינדקס מספרי.
הוא אינדקס מספרי.![plot:\[{F_{n,\alpha }}\]](/documentResources/326/plot_12.png) .
. ![plot:\[n\]](/documentResources/326/plot_13.png) הוא מספר הארגומנטים ביחס ו-
הוא מספר הארגומנטים ביחס ו-![plot:\[\alpha \]](/documentResources/326/plot_14.png) הוא אינדקס מספרי.
הוא אינדקס מספרי.![plot:\[\tau \]](/documentResources/326/plot_15.png) .
לדוגמא:
.
לדוגמא: ![plot:\[{\tau _0} = \left\langle
{{R_{1,0}},{R_{1,1}},{F_{2,0}},{F_{2,3}},{C_2},{C_3}} \right\rangle \]](/documentResources/326/plot_16.png) .
.![plot:\[ \cup \]](/documentResources/326/plot_17.png) קבועים)X.
קבועים)X.![plot:\[\left\{ {{v_i}|i \in \mathbb{N}}
\right\}\]](/documentResources/326/plot_18.png) .
.![plot:\[{F_{n,\alpha }}\]](/documentResources/326/plot_19.png) במילון נגדיר פעולה המקבלת
שמות עצם
במילון נגדיר פעולה המקבלת
שמות עצם ![plot:\[{t_1},...,{t_n}\]](/documentResources/326/plot_20.png) ומוציאה כפלט את
ומוציאה כפלט את ![plot:\[{F_{n,\alpha }}\left( {{t_1},...,{t_n}} \right)\]](/documentResources/326/plot_21.png) .
.![plot:\[{R_{n,\alpha }}\left( {{t_1},...,{t_n}}
\right)\]](/documentResources/326/plot_22.png) כאשר
כאשר ![plot:\[{t_1},...,{t_n}\]](/documentResources/326/plot_23.png) שמות עצם, ו-
שמות עצם, ו-![plot:\[{R_{n,\alpha }}\]](/documentResources/326/plot_24.png) הינו סימן יחס
הינו סימן יחס ![plot:\[n\]](/documentResources/326/plot_25.png) -מקומי מהמילון. כל סדרת סימנים כזו תקרא נוסחה
אטומית.
-מקומי מהמילון. כל סדרת סימנים כזו תקרא נוסחה
אטומית.![plot:\[F\left( {x,x} \right) = F\left( {x,y}
\right)\]](/documentResources/326/plot_26.png) זוהי נוסחה אטומית.
זוהי נוסחה אטומית.![plot:\[\alpha ,\beta \]](/documentResources/326/plot_27.png) נוסחאות, אזי גם
הביטויים הנ"ל הם נוסחאות:
נוסחאות, אזי גם
הביטויים הנ"ל הם נוסחאות: ![plot:\[\left( {\alpha \wedge \beta } \right),\left(
{\alpha \vee \beta } \right),\left(
{\alpha \to \beta } \right),\left(
{\neg \alpha } \right)\]](/documentResources/326/plot_28.png) .
.![plot:\[\alpha \]](/documentResources/326/plot_29.png) ומשתנה
ומשתנה ![plot:\[x\]](/documentResources/326/plot_30.png) ,
גם
,
גם ![plot:\[\forall x\alpha \]](/documentResources/326/plot_31.png) ו-
ו-![plot:\[\exists x\alpha \]](/documentResources/326/plot_32.png) הן נוסחאות.
הן נוסחאות.![plot:\[\forall {v_i}P\left( {{v_i}} \right) \to R\left( {{v_r}} \right) \equiv
\left( {\forall {v_i}P\left( {{v_i}} \right)} \right) \to R\left( {{v_r}}
\right)\]](/documentResources/326/plot_33.png)
![plot:\[F\left( {F\left( {} \right)} \right)\]](/documentResources/326/plot_34.png) הינו שם עצם.
הינו שם עצם. ![plot:\[R\left( {R\left( {} \right)} \right)\]](/documentResources/326/plot_35.png) לא מוגדר כחלק מתחשיב היחסים!
לא מוגדר כחלק מתחשיב היחסים!![plot:\[R\left( {F\left( {} \right)} \right)\]](/documentResources/326/plot_36.png) הינה נוסחה אטומית.
הינה נוסחה אטומית. ![plot:\[F\left( {R\left( {} \right)} \right)\]](/documentResources/326/plot_37.png) לא קיים – אסור להפעיל סימני פונקציה על יחס.
לא קיים – אסור להפעיל סימני פונקציה על יחס.![plot:\[R \to R\]](/documentResources/326/plot_38.png) מותר.
מותר. ![plot:\[F \to F\]](/documentResources/326/plot_39.png) - אסור. יש לתת סימני יחס בין הקשרים והכמתים.
- אסור. יש לתת סימני יחס בין הקשרים והכמתים.![plot:\[\forall xR\]](/documentResources/326/plot_40.png) מותר.
מותר. ![plot:\[\forall xF\]](/documentResources/326/plot_41.png) אסור.
אסור.![plot:\[\tau \]](/documentResources/326/plot_42.png) ,
,
![plot:\[\tau
= \left\langle {{R_1},...,{R_m},{F_1},...,{F_k},{C_1}...,{C_l}}
\right\rangle \]](/documentResources/326/plot_43.png) מבנה עבור
מבנה עבור ![plot:\[\tau \]](/documentResources/326/plot_44.png) מוגדר כך:
מוגדר כך:![plot:\[M
= \left\langle {{D^M},{R_1}^M,...,{R_m}^M,{F^M}_1,...,{F_k}^M,{C_1}^M...,{C_l}^M}
\right\rangle \]](/documentResources/326/plot_45.png)
![plot:\[{D^M}\]](/documentResources/326/plot_46.png) הוא התחום,
הוא התחום, ![plot:\[{R_i}^M\]](/documentResources/326/plot_47.png) הוא הפירוש של סימן היחס
הוא הפירוש של סימן היחס ![plot:\[{R_i}\]](/documentResources/326/plot_48.png) במבנה
במבנה ![plot:\[M\]](/documentResources/326/plot_49.png) ,
, ![plot:\[{F_i}^M\]](/documentResources/326/plot_50.png) הוא הפירוש של סימן הפונקציה
הוא הפירוש של סימן הפונקציה ![plot:\[{F_i}\]](/documentResources/326/plot_51.png) במבנה
במבנה ![plot:\[M\]](/documentResources/326/plot_52.png) ,
, ![plot:\[{C_i}^M\]](/documentResources/326/plot_53.png) הוא הפירוש של סימן הקבוע
הוא הפירוש של סימן הקבוע ![plot:\[{C_i}\]](/documentResources/326/plot_54.png) במבנה
במבנה ![plot:\[M\]](/documentResources/326/plot_55.png) .
.![plot:\[\tau = \left\langle
{{R_{2,0}},{F_{1,0}},{C_0},{C_1}} \right\rangle \]](/documentResources/326/plot_56.png) .
. ![plot:\[{M_2} = \left\langle {P\left( A \right),
\subseteq ,{\text{completion}},\phi ,A} \right\rangle ,{M_1} = \left\langle
{\mathbb{N}, \leqslant , + 1,2,3} \right\rangle \]](/documentResources/326/plot_57.png) .
.![plot:\[\tau \]](/documentResources/326/plot_58.png) ,
נגדיר השמה
,
נגדיר השמה ![plot:\[z\]](/documentResources/326/plot_59.png) המתאימה למשתנים ערכים מהתחום:
המתאימה למשתנים ערכים מהתחום:![plot:\[z:\left\{
{{v_i}|i \in \mathbb{N}} \right\} \to {D^M}\]](/documentResources/326/plot_60.png)
![plot:\[z\]](/documentResources/326/plot_61.png) ,
שתתאים לכל שם עצם
,
שתתאים לכל שם עצם ![plot:\[t\]](/documentResources/326/plot_62.png) מעל המילון
מעל המילון ![plot:\[\tau \]](/documentResources/326/plot_63.png) איבר בתחום שיסומן
איבר בתחום שיסומן ![plot:\[\bar z\left( t \right)\]](/documentResources/326/plot_64.png) .
.![plot:\[t\]](/documentResources/326/plot_65.png) משתנה
משתנה![plot:\[\bar z\left( t \right) = z\left( t
\right) \Leftarrow \]](/documentResources/326/plot_66.png) .
. ![plot:\[t\]](/documentResources/326/plot_67.png) קבוע
קבוע![plot:\[\bar z\left( {{c_i}} \right) = {c_i}^M
\Leftarrow t = {c_i} \Leftarrow \]](/documentResources/326/plot_68.png) .
.![plot:\[\bar z\left( {{F_{n,\alpha }}\left(
{{t_1},...,{t_n}} \right)} \right) = F_{n,\alpha }^M\left( {\bar z\left(
{{t_1}} \right),...,\bar z\left( {{t_n}} \right)} \right)\]](/documentResources/326/plot_69.png) .
.![plot:\[\forall {v_1}{R_{2,0}}\left(
{{v_1},{v_1}} \right)\]](/documentResources/326/plot_70.png) - כל האיברים בתחום הם ביחס עם עצמם.
- כל האיברים בתחום הם ביחס עם עצמם.![plot:\[{R_{2,0}}\left( {{v_1},{v_1}} \right)\]](/documentResources/326/plot_71.png) -
- ![plot:\[{v_1}\]](/documentResources/326/plot_72.png) ביחס
ביחס ![plot:\[{R_{2,0}}\]](/documentResources/326/plot_73.png) עם עצמו.
עם עצמו.![plot:\[{v_1}\]](/documentResources/326/plot_74.png) בהשמה, ובנוסחה השניה כן. בנוסחה הראשונה
בהשמה, ובנוסחה השניה כן. בנוסחה הראשונה ![plot:\[{v_1}\]](/documentResources/326/plot_75.png) מופיע קשור (תחת השפעת הכמת), לכן הוא אינו מופיע בתרגום הנוסחה למילים ואין צורך
לדעת את הערך שההשמה נתנה לו. בנוסחה השניה
מופיע קשור (תחת השפעת הכמת), לכן הוא אינו מופיע בתרגום הנוסחה למילים ואין צורך
לדעת את הערך שההשמה נתנה לו. בנוסחה השניה ![plot:\[{v_1}\]](/documentResources/326/plot_76.png) חופשי.
חופשי.![plot:\[\alpha \]](/documentResources/326/plot_77.png) נוסחה מעל מילון
נוסחה מעל מילון ![plot:\[\tau \]](/documentResources/326/plot_78.png) ו-
ו-![plot:\[M\]](/documentResources/326/plot_79.png) מבנה עבור
מבנה עבור ![plot:\[\tau \]](/documentResources/326/plot_80.png) . אם
. אם ![plot:\[{z_1}\]](/documentResources/326/plot_81.png) ו-
ו-![plot:\[{z_2}\]](/documentResources/326/plot_82.png) השמות ב-
השמות ב-![plot:\[M\]](/documentResources/326/plot_83.png) המזדהות על המשתנים החופשיים ב-
המזדהות על המשתנים החופשיים ב-![plot:\[\alpha \]](/documentResources/326/plot_84.png) ,
אז ערך האמת של
,
אז ערך האמת של ![plot:\[\alpha \]](/documentResources/326/plot_85.png) תחת
תחת ![plot:\[{z_1}\]](/documentResources/326/plot_86.png) ותחת
ותחת![plot:\[{z_2}\]](/documentResources/326/plot_87.png) זהה.
זהה.![plot:\[\alpha \]](/documentResources/326/plot_88.png) נוסחה ללא משתנים חופשיים, אז ערך האמת של
נוסחה ללא משתנים חופשיים, אז ערך האמת של ![plot:\[\alpha \]](/documentResources/326/plot_89.png) אינו תלוי בהשמה.
אינו תלוי בהשמה.![plot:\[\alpha \]](/documentResources/326/plot_90.png) בלי משתנים חופשיים נקראת פסוק.
בלי משתנים חופשיים נקראת פסוק.![plot:\[\alpha \]](/documentResources/326/plot_91.png) מתי
מתי ![plot:\[{v_i}\]](/documentResources/326/plot_92.png) הוא משתנה חופשי ב-
הוא משתנה חופשי ב-![plot:\[\alpha \]](/documentResources/326/plot_93.png) .
.![plot:\[{v_i}\]](/documentResources/326/plot_94.png) חופשי ב-
חופשי ב-![plot:\[\alpha \]](/documentResources/326/plot_95.png) אם
אם ![plot:\[{v_i}\]](/documentResources/326/plot_96.png) מופיע ב-
מופיע ב-![plot:\[\alpha \]](/documentResources/326/plot_97.png) .
.![plot:\[ \circ
\in \left\{ { \wedge , \vee , \to } \right\}\]](/documentResources/326/plot_98.png) ,
, ![plot:\[{v_i}\]](/documentResources/326/plot_99.png) חופשי ב-
חופשי ב-![plot:\[\left( {\alpha \circ \beta } \right)\]](/documentResources/326/plot_100.png) אם
אם ![plot:\[{v_i}\]](/documentResources/326/plot_101.png) חופשי ב-
חופשי ב-![plot:\[\alpha \]](/documentResources/326/plot_102.png) או
או ![plot:\[{v_i}\]](/documentResources/326/plot_103.png) חופשי ב-
חופשי ב-![plot:\[\beta \]](/documentResources/326/plot_104.png) .
.![plot:\[{v_i}\]](/documentResources/326/plot_105.png) חופשי ב-
חופשי ב-![plot:\[\left( {\neg \alpha } \right)\]](/documentResources/326/plot_106.png) אם
אם ![plot:\[{v_i}\]](/documentResources/326/plot_107.png) חופשי ב-
חופשי ב-![plot:\[\alpha \]](/documentResources/326/plot_108.png) .
.![plot:\[{v_i}\]](/documentResources/326/plot_109.png) חופשי ב-
חופשי ב-![plot:\[\forall {v_j}\alpha \]](/documentResources/326/plot_110.png) או ב-
או ב-![plot:\[\exists {v_j}\alpha \]](/documentResources/326/plot_111.png) אם
אם ![plot:\[{v_i}\]](/documentResources/326/plot_112.png) חופשי ב-
חופשי ב-![plot:\[\alpha \]](/documentResources/326/plot_113.png) וגם
וגם ![plot:\[i \ne j\]](/documentResources/326/plot_114.png) .
.![plot:\[\tau \]](/documentResources/326/plot_115.png) :
: ![plot:\[\tau
= \left\langle {{R_1},...,{R_m},{F_1},...,{F_k},{C_1},...,{C_l}}
\right\rangle \]](/documentResources/326/plot_116.png) מבנה עבור
מבנה עבור ![plot:\[\tau \]](/documentResources/326/plot_117.png) הוא:
הוא:![plot:\[M
= \left\langle
{{D^M},{R_1}^M,...,{R_m}^M,{F^M}_1,...,{F_k}^M,{C_1}^M...,{C_l}^M}
\right\rangle \]](/documentResources/326/plot_118.png)
![plot:\[{D^M}\]](/documentResources/326/plot_119.png) הוא התחום.
הוא התחום.![plot:\[1 \leqslant i \leqslant m\]](/documentResources/326/plot_120.png) אם
אם ![plot:\[{R_i}\]](/documentResources/326/plot_121.png) הוא סימן יחס
הוא סימן יחס ![plot:\[n\]](/documentResources/326/plot_122.png) -מקומי
אזי
-מקומי
אזי ![plot:\[R_i^M \subseteq \underbrace {{D^M}
\times ... \times {D^M}}_{n{\text{ times}}}\]](/documentResources/326/plot_123.png) , כלומר
, כלומר ![plot:\[R_i^M\]](/documentResources/326/plot_124.png) הוא יחס
הוא יחס ![plot:\[n\]](/documentResources/326/plot_125.png) -מקומי
מעל
-מקומי
מעל ![plot:\[{D^M}\]](/documentResources/326/plot_126.png) .
.![plot:\[1 \leqslant i \leqslant k\]](/documentResources/326/plot_127.png) אם
אם ![plot:\[{F_i}\]](/documentResources/326/plot_128.png) סימן פונקציה
סימן פונקציה ![plot:\[n\]](/documentResources/326/plot_129.png) -מקומי
אז
-מקומי
אז ![plot:\[F_i^M:\underbrace {{D^M} \times
... \times {D^M}}_{n{\text{ times}}} \to {D^M}\]](/documentResources/326/plot_130.png) , כלומר
, כלומר ![plot:\[F_i^M\]](/documentResources/326/plot_131.png) מתארת מה הערך של
מתארת מה הערך של ![plot:\[{F_i}\]](/documentResources/326/plot_132.png) עבור כל
עבור כל ![plot:\[n\]](/documentResources/326/plot_133.png) -יה סדורה של איברים מ-
-יה סדורה של איברים מ-![plot:\[{D^M}\]](/documentResources/326/plot_134.png) .
.![plot:\[1 \leqslant i \leqslant l\]](/documentResources/326/plot_135.png) , מתקיים:
, מתקיים: ![plot:\[C_i^M \in {D^M}\]](/documentResources/326/plot_136.png) .
.![plot:\[z\]](/documentResources/326/plot_137.png) ב-
ב-![plot:\[M\]](/documentResources/326/plot_138.png) :
: ![plot:\[z:\left\{ {{v_i}|i \in \mathbb{N}}
\right\} \to {D^M}\]](/documentResources/326/plot_139.png) וראינו כיצד להרחיב את
וראינו כיצד להרחיב את ![plot:\[z\]](/documentResources/326/plot_140.png) כך שתתאים ערך מהתחום לכל שם עצם.
כך שתתאים ערך מהתחום לכל שם עצם.![plot:\[\alpha \]](/documentResources/326/plot_141.png) מעל מילון
מעל מילון ![plot:\[\tau \]](/documentResources/326/plot_142.png) , מבנה
, מבנה ![plot:\[M\]](/documentResources/326/plot_143.png) והשמה
והשמה ![plot:\[z\]](/documentResources/326/plot_144.png) עבור
עבור ![plot:\[M\]](/documentResources/326/plot_145.png) נסמן
נסמן ![plot:\[M\mathop \vDash \limits_z \alpha \]](/documentResources/326/plot_146.png) את הטענה ש-
את הטענה ש-![plot:\[\alpha \]](/documentResources/326/plot_147.png) מסתפקת ב-
מסתפקת ב-![plot:\[M\]](/documentResources/326/plot_148.png) תחת
תחת ![plot:\[z\]](/documentResources/326/plot_149.png) .
.![plot:\[\alpha \]](/documentResources/326/plot_150.png) מתי
מתי ![plot:\[M\mathop \vDash \limits_z \alpha \]](/documentResources/326/plot_151.png) .
.![plot:\[\alpha \]](/documentResources/326/plot_152.png) נוסחה אטומית:
נוסחה אטומית: ![plot:\[\alpha
= \left( {{t_1} \approx {t_2}} \right)\]](/documentResources/326/plot_153.png) עבור
עבור ![plot:\[{t_1},{t_2}\]](/documentResources/326/plot_154.png) שמות עצם,
שמות עצם, ![plot:\[M\mathop \vDash \limits_z
\alpha \Leftrightarrow \bar z\left( {{t_1}}
\right) = \bar z\left( {{t_2}} \right)\]](/documentResources/326/plot_155.png) .
.![plot:\[\alpha = R\left(
{{t_1},...,{t_n}} \right)\]](/documentResources/326/plot_156.png) , עבור
, עבור ![plot:\[{t_1},...,{t_n}\]](/documentResources/326/plot_157.png) שמות עצם,
שמות עצם, ![plot:\[M\mathop \vDash \limits_z
\alpha \Leftrightarrow \left( {\bar
z\left( {{t_1}} \right),...,\bar z\left( {{t_n}} \right)} \right) \in {R^M}\]](/documentResources/326/plot_158.png) .
.![plot:\[\alpha \]](/documentResources/326/plot_159.png) , מבנה
, מבנה ![plot:\[M\]](/documentResources/326/plot_160.png) והשמה
והשמה ![plot:\[z\]](/documentResources/326/plot_161.png) , מתקיים כי
, מתקיים כי ![plot:\[M\mathop \vDash \limits_z \alpha \]](/documentResources/326/plot_162.png) או
או ![plot:\[M\mathop \vDash \limits_z
\neg \alpha \]](/documentResources/326/plot_163.png) אבל לא שניהם.
אבל לא שניהם.![plot:\[M'\]](/documentResources/326/plot_164.png) והשמה
והשמה ![plot:\[z'\]](/documentResources/326/plot_165.png) אנו יודעים האם
אנו יודעים האם ![plot:\[M'\mathop \vDash
\limits_{z'} \alpha \]](/documentResources/326/plot_166.png) . נרצה לדעת האם
. נרצה לדעת האם ![plot:\[M\mathop \vDash \limits_z \forall {v_i}\alpha \]](/documentResources/326/plot_167.png) ,
, ![plot:\[M\mathop \vDash \limits_z
\exists {v_i}\alpha \]](/documentResources/326/plot_168.png) למבנה והשמה מסויימים. בהינתן השמה
למבנה והשמה מסויימים. בהינתן השמה ![plot:\[z\]](/documentResources/326/plot_169.png) ,
משתנה
,
משתנה ![plot:\[{v_i}\]](/documentResources/326/plot_170.png) ואיבר
ואיבר ![plot:\[d \in {D^M}\]](/documentResources/326/plot_171.png) , נגדיר השמה מתוקנת
, נגדיר השמה מתוקנת ![plot:\[z\left[ {{v_i} \leftarrow d} \right]\]](/documentResources/326/plot_172.png) :
:![plot:\[z\left[ {{v_i} \leftarrow d}
\right]\left( {{v_j}} \right) = \left\{ {\begin{array}{*{20}{c}}
{z\left( {{v_j}} \right)} \hfill & {i \ne j} \hfill \\
d \hfill & {i = j} \hfill \\
\end{array} } \right.\]](/documentResources/326/plot_173.png)
![plot:\[d \in {D^M}\]](/documentResources/326/plot_174.png) מתקיים
מתקיים ![plot:\[M\mathop \vDash \limits_z \forall {v_i}\alpha \Leftrightarrow M\mathop \vDash \limits_{z\left[ {{v_i} \leftarrow d}
\right]} \alpha \]](/documentResources/326/plot_175.png) .
.![plot:\[d \in {D^M}\]](/documentResources/326/plot_176.png) עבורו
עבורו ![plot:\[M\mathop \vDash \limits_z \exists {v_i}\alpha \Leftrightarrow M\mathop \vDash \limits_{z\left[ {{v_i} \leftarrow d}
\right]} \alpha \]](/documentResources/326/plot_177.png) .
.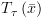 ושל
ושל