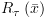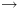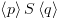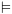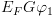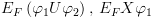6.5.4. BDD כמבנה נתונים
BDD עבור פונקציה בוליאנית 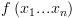 הינו גרף מכוון חסר מעגלים עם שורש ושני סוגי
צמתים: צמתי קצה וצמתים פנימיים. שורש העץ יכול להיות צומת קצה או צומת פנימי.
הינו גרף מכוון חסר מעגלים עם שורש ושני סוגי
צמתים: צמתי קצה וצמתים פנימיים. שורש העץ יכול להיות צומת קצה או צומת פנימי.
לצומת פנימי 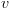 יש את השדות הבאים:
יש את השדות הבאים:
- משתנה
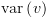
- שני מצביעים:
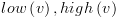 .
.
לצומת קצה יש ערך בודד: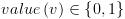
על מנת להבטיח יצוג קנוני נוסיף את
התנאים הבאים:
- כל משתנה מופיע פעם אחת לכל היותר על כל מסלול מהשורש לעלה.
- נגדיר סדר למשתנים. המשתנים מופיעים באותו סדר לאורך כל מסלול מהשורש
לעלה (לא בהכרח כולם מופיעים). מוסכמה – הסדר הינו סדר עולה מהשורש לעלים.
- הגרף אינו מכיל תתי גרפים איזומורפיים או צמתים מיותרים (שאין תלות
בערך המשתנה בהם על המסלול המסוים).
עם מגבלות אלו מתקבל Reduced Ordered BDD
(ROBDD). בהמשך,
כאשר נדבר על BDD נתכוון תמיד ל-ROBDD.
עבור ROBDD בהינתן סדר מסויים של המשתנים,
לכל הפונקציות השקולות זו לזו יש ייצוג זהה עד כדי איזומורפיזם.
בהינתן BDD – איזו פונקציה הוא מגדיר:
בהינתן BDD עם שורש 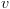 הוא מגדיר פונקציה
הוא מגדיר פונקציה 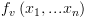 באופן הבא:
באופן הבא:
- אם
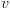 צומת קצה -
צומת קצה - ![plot:\[{f_v}\left( {{x_1}...{x_n}} \right) = value\left( v
\right)\]](/documentResources/326/plot_217.png)
- אם
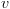 אינו צומת קצה ואם
אינו צומת קצה ואם 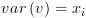 אזי:
אזי:
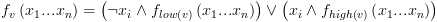
נמשיך עם שרטוט הדוגמא:
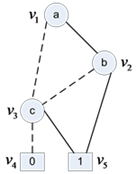
נחשב את 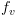 עבור ה-BDD:
עבור ה-BDD:
מתקיים: 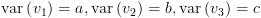 וכמו כן
וכמו כן 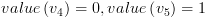 .
.
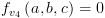
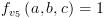
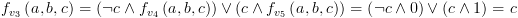
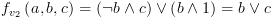
![plot:\[{f_{{v_1}}}\left(
{a,b,c} \right) = \left( {\neg a \wedge c} \right) \vee \left( {a \wedge \left(
{b \vee c} \right)} \right) = \left( {a \wedge b} \right) \vee c\]](/documentResources/326/plot_218.png)
עובדות על BDD:
- כל צומת ב-BDD מייצג איזשהו "זכרון".
- לא לכל פונקציה בוליאנית קיים BDD "קטן"
פולינומיאלית במספר משתני הפונקציה. יש
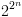 פונקציות בוליאניות עם
פונקציות בוליאניות עם 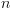 משתנים, ויש הרבה פחות DAG בגודל פולינומיאלי ב-
משתנים, ויש הרבה פחות DAG בגודל פולינומיאלי ב-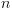 .
.
- לפונקצית הכופל אין BDD פולינומיאלי לכל סדר שהוא.
פונקצית הכופל היא הפונקציה
המקבלת שני מספרים 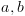 ביצוג בינארי:
ביצוג בינארי: 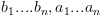 ומחזירה את המכפלה שלהם
ומחזירה את המכפלה שלהם  ביצוג
ביצוג 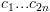 .
.
- מציאת הסדר האופטימלי של המשתנים ב-BDD היא בעיית NP-קשה.


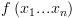 הינו גרף מכוון חסר מעגלים עם שורש ושני סוגי
צמתים: צמתי קצה וצמתים פנימיים. שורש העץ יכול להיות צומת קצה או צומת פנימי.
הינו גרף מכוון חסר מעגלים עם שורש ושני סוגי
צמתים: צמתי קצה וצמתים פנימיים. שורש העץ יכול להיות צומת קצה או צומת פנימי.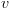 יש את השדות הבאים:
יש את השדות הבאים: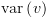
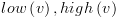 .
.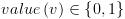
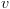 הוא מגדיר פונקציה
הוא מגדיר פונקציה 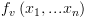 באופן הבא:
באופן הבא: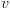 צומת קצה -
צומת קצה - ![plot:\[{f_v}\left( {{x_1}...{x_n}} \right) = value\left( v
\right)\]](/documentResources/326/plot_217.png)
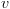 אינו צומת קצה ואם
אינו צומת קצה ואם 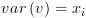 אזי:
אזי: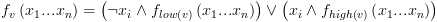

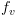 עבור ה-BDD:
עבור ה-BDD: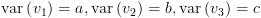 וכמו כן
וכמו כן 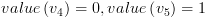 .
.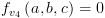
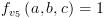
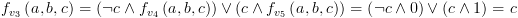
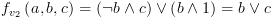
![plot:\[{f_{{v_1}}}\left(
{a,b,c} \right) = \left( {\neg a \wedge c} \right) \vee \left( {a \wedge \left(
{b \vee c} \right)} \right) = \left( {a \wedge b} \right) \vee c\]](/documentResources/326/plot_218.png)
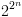 פונקציות בוליאניות עם
פונקציות בוליאניות עם 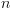 משתנים, ויש הרבה פחות DAG בגודל פולינומיאלי ב-
משתנים, ויש הרבה פחות DAG בגודל פולינומיאלי ב-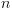 .
.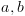 ביצוג בינארי:
ביצוג בינארי: 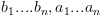 ומחזירה את המכפלה שלהם
ומחזירה את המכפלה שלהם  ביצוג
ביצוג 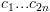 .
.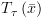 ושל
ושל