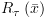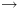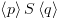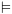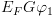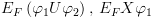4.2. סמנטיקההמטרה שלנו: הגדרת חישוב של תוכנית. לצורך כך נגדיר את מושג הקונפיגורציה ואת רלציית המעברים: קונפיגורציה – זוג משמעות קונפיגורציה: הפקודה שנמצאת
בצומת עם התווית רלציית המעברים
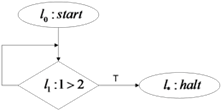
בנוסף: כאשר ב- הארה: רלצית המעברים לוקחת את גרף תרשימי הזרימה ונותנת לנו את היכולת להשתמש בו ככלי לניתוח התוכנית. היא מאפשרת לנו לעשות בו צעדים רק בהתאם לתוכנית עצמה. הגדרת חישוב: חישוב של תוכנית P מקונפיגורציה C מסומן חישוב סופי תמיד יסתיים בקונפיגורציה עוצרת. קונפיגורציה עוצרת: קונפיגורציה התחלתית: עבור חישוב סופי בהינתן חישוב בתוכנית יש מסלול יחיד שמתאים לו. בהינתן מסלול יכול להיות שאין חישוב שמתאים לו, או לחילופין יכולים להיות אין סוף חישובים מתאימים.
אין תגובות!
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


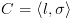 כאשר
כאשר 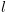 תווית המציינת את הצומת בתוכנית בו נמצא החישוב.
תווית המציינת את הצומת בתוכנית בו נמצא החישוב. 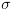 הינו מצב (השמה למשתנים).
הינו מצב (השמה למשתנים).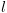 מתבצעת ממצב
מתבצעת ממצב 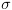 .
.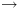 בין קונפיגורציות
בין קונפיגורציות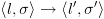 אמ"מ קיימת קשת מ-
אמ"מ קיימת קשת מ-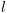 ל-
ל-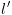 בתוכנית ובנוסף מתקיים אחד מהתנאים הבאים:
בתוכנית ובנוסף מתקיים אחד מהתנאים הבאים: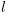 יש פונקצית אתחול וגם
יש פונקצית אתחול וגם 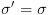 .
.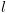 פקודת הצבה מהצורה
פקודת הצבה מהצורה 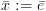 ומתקיים
ומתקיים ![plot:$\sigma ' = \sigma \left[ {\bar x
\leftarrow \sigma \left( {\bar e} \right)} \right]$](/documentResources/326/plot_430.png) .
.![plot:$\sigma ' = \sigma \left[ {\bar x
\leftarrow \sigma \left( {\bar e} \right)} \right]$](/documentResources/326/plot_431.png) הינה הצבה חלקית,
בה מוחלפים ב-
הינה הצבה חלקית,
בה מוחלפים ב-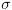 כל ערכי המשתנים
המצוינים בווקטור.
כל ערכי המשתנים
המצוינים בווקטור.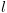 פונקצית בדיקה
פונקצית בדיקה 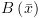 , מתקיים
, מתקיים 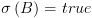 וגם קיימת קשת מ-
וגם קיימת קשת מ-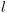 ל-
ל-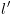 בתוכנית המסומנת
בתוכנית המסומנת 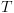 ,
וכן
,
וכן 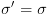 או
או 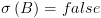 וגם קיימת קשת מ-
וגם קיימת קשת מ-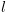 ל-
ל-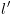 בתוכנית המסומנת
בתוכנית המסומנת 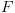 ,
וכן
,
וכן 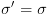 .
.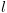 יש halt אין מעבר לאף קונפיגורציה
אחרת.
יש halt אין מעבר לאף קונפיגורציה
אחרת.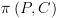 הינו סידרה מקסימלית של
קונפיגורציות
הינו סידרה מקסימלית של
קונפיגורציות 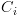 כך ש-
כך ש-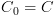 ולכל
ולכל 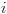 מתקיים
מתקיים 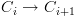 .
.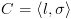 היא קונפיגורציה עוצרת אם
היא קונפיגורציה עוצרת אם 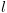 מציינת צומת עצירה בתוכנית.
מציינת צומת עצירה בתוכנית.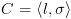 היא קונפיגורציה התחלתית אם
היא קונפיגורציה התחלתית אם 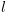 מציינת את צומת האתחול בתוכנית.
מציינת את צומת האתחול בתוכנית.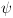 המסתיים בקונפיגורציה (עוצרת)
המסתיים בקונפיגורציה (עוצרת) 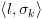 מגדירים את
מגדירים את 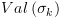 להיות
להיות 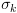 .
.
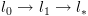
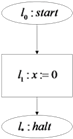
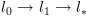
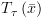 ושל
ושל