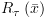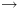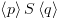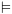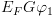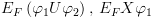6.5.5.3. פעולות בוליאניות על BDD (Apply)בהינתן שני BDD: נסתמך על "הרחבת
Shonon": Apply עובדת לפי ארבעה מקרים שונים:
(חישוב
דוגמא:
נחשב את
ואחרי צמצום:
דוגמא יהיו 2 פונקציות הפונקציות עצמן הינן:
נרצה לחשב את הפונקציה
ומכאן נקבל:
אנו מקבלים כי:
ניתן להגיע לאותו הפיתוח באמצעות שימוש בלוגיקה, לבדיקה:
סיבוכיות פעולה APPLY טיפול פשטני נותן לנו פתרון
אקספוננציאלי בגודל ה-BDD. כדי לפתור את הבעיה ביעילות נשים לב כי כל צומת ב-BDD
מייצג פונקציה, ומספר הפונקציות השונות שמיוצגות הוא כמספר הצמתים נשתמש בטבלת HASH: לכל הפעלה של APPLY יש מצביעים לצמתים ב-BDD שמהם הפעולה הופעלה, וכן את הפעולה שהופעלה. לא נבצע את אותו חישוב פעמיים אלא נשתמש בתוצאות שכבר חישבנו. כעת הסיבוכיות תלויה בכמות פעולות ה-APPLY
השונות שמבצעים במהלך תהליך APPLY על
אין תגובות!
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


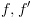 נרצה לחשב את ה-BDD של
נרצה לחשב את ה-BDD של 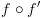 כאשר
כאשר  הוא אחת מ-16 הפונקציות הבינאריות. סימונים:
הוא אחת מ-16 הפונקציות הבינאריות. סימונים: 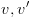 הם השורשים של
הם השורשים של 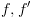 בהתאמה. אם
בהתאמה. אם 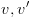 אינם צמתי קצה אז
אינם צמתי קצה אז 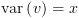 וכן
וכן 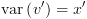 .
.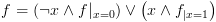
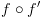 ):
):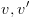 הם צמתי קצה אז תוצאת הפעולה היא
הם צמתי קצה אז תוצאת הפעולה היא 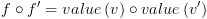
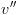 כך שמתקיים
כך שמתקיים 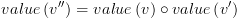
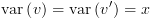 אז
אז ![plot:\[f \circ f' = \left( {\neg x \wedge
\left( {f{|_{x = 0}} \circ f'{|_{x = 0}}} \right)} \right) \vee \left( {x
\wedge \left( {f{|_{x = 1}} \circ f'{|_{x = 1}}} \right)} \right)\]](/documentResources/326/plot_220.png) .
.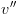 כך שיתקיים:
כך שיתקיים: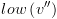 יצביע אל ה-BDD:
יצביע אל ה-BDD: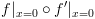
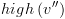 יצביע אל ה-BDD:
יצביע אל ה-BDD:
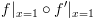 .
.
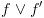 :
:

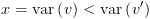 כאשר היחס
כאשר היחס 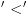 מוגדר על סדר נתון, (כלומר
מוגדר על סדר נתון, (כלומר 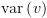 לא מופיע ב
לא מופיע ב 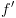 או בניסוח אחר:
או בניסוח אחר: 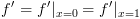 ) אז:
) אז: 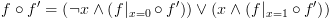
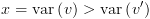 .
.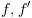 מעל המשתנים
מעל המשתנים 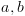 . נקבע את סדר המשתנים להיות
. נקבע את סדר המשתנים להיות 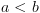 .
.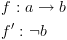
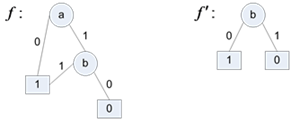
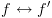 . המקרה כאן הוא מקרה 3.
. המקרה כאן הוא מקרה 3.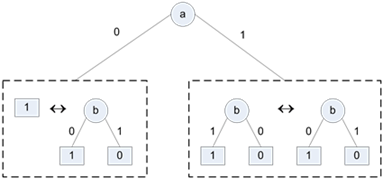
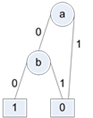
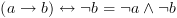
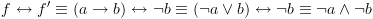
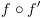 . נסמן ב-
. נסמן ב-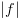 את מספר הצמתים ב-BDD של
את מספר הצמתים ב-BDD של 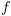 ומכאן: מספר הפעולות הוא
ומכאן: מספר הפעולות הוא 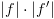 .
.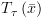 ושל
ושל