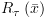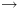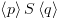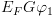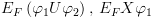4.4.5.2. דוגמא להפעלת Floydנציג שוב את התוכנית המחשבת את המנה
והשארית של חלוקת
הפעלת Floyd:
נציב בתנאי:
קיבלנו נוסחה בלוגיקה. לצורך הוכחת אימות תוכנה מספיק לנו לראות שהנוסחה נכונה מבחינה מתמטית – אין צורך להכנס להוכחה מורכבת בלוגיקה. ממתמטיקה טריויאלית ניתן לראות את נכונות הביטוי.
אין תגובות!
|
תוכן העניינים:
קישורים רלוונטיים:שיתוף: |


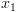 ב-
ב-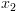 . בשרטוט הצומת
. בשרטוט הצומת  אינו עושה דבר וקיים רק לצרכי
פישוט ההוכחה. ניתן להוכיח את התוכנית גם בלעדיו.
אינו עושה דבר וקיים רק לצרכי
פישוט ההוכחה. ניתן להוכיח את התוכנית גם בלעדיו.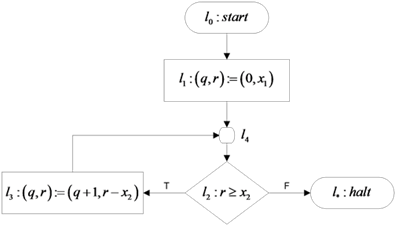
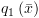 ואת
ואת 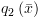 :
: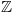 .
.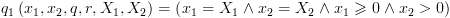
 את הטענה
את הטענה 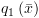 ונצמיד ל-
ונצמיד ל-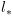 את הטענה
את הטענה 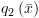 .
.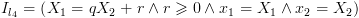 . אם האינוריאנטה מתקיימת ובחרנו לצאת
מהלולאה, הרי שהטענה תבטיח את
. אם האינוריאנטה מתקיימת ובחרנו לצאת
מהלולאה, הרי שהטענה תבטיח את 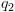 בסיום, ולכן זו נראית טענה מוצלחת.
בסיום, ולכן זו נראית טענה מוצלחת.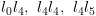 .
. 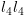 .
.![plot:${I_l}_{_4}\left( {\bar x} \right) \wedge
{R_{{l_4}{l_4}}}\left( {\bar x} \right) \to {I_{{l_4}}}\left[ {\bar x
\leftarrow {T_{{l_4}{l_4}}}\left( {\bar x} \right)} \right]$](/documentResources/326/plot_595.png)
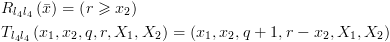
![plot:\[\begin{gathered}
\left( {{X_1} = q{X_2} + r \wedge r \geqslant 0 \wedge {x_1} = {X_1}
\wedge {x_2} = {X_2}} \right) \wedge \left( {r \geqslant {x_2}} \right)
\to \hfill \\
\left( {{X_1} = \left( {q + 1} \right){X_2} + \left( {r - {X_2}} \right)
\wedge r - {X_2} \geqslant 0 \wedge {x_1} = {X_1} \wedge {x_2} = {X_2}} \right)
\hfill \\
\end{gathered} \]](/documentResources/326/plot_185.png)
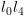 ו-
ו-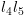 יחושבו בצורה דומה.
יחושבו בצורה דומה.![plot:\[{ \vdash
_F}\left\{ {{q_1}} \right\}P\left\{ {{q_2}} \right\}\]](/documentResources/326/plot_186.png) .
.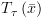 ושל
ושל