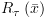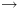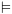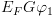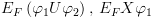4.4.5. כלל ההוכחה F ( (Floyd לתוכניות תרשים זרימה עם חוגים
כלל ההוכחה של Floyd משמש אותנו להוכחת 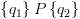 . נשתמש בכלל הבא:
. נשתמש בכלל הבא:
- נבחר "נקודות חתך" בתוכנית בצורה הבאה:
א.
נקודת ההתחלה 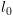
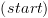 תהיה נקודת חתך.
תהיה נקודת חתך.
ב.
נקודת הסיום 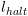
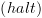 תהיה נקודת חתך.
תהיה נקודת חתך.
ג.
כל מעגל בגרף התוכנית יכיל לפחות נקודת חתך אחת.
- לכל נקודת חתך
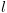 , נמצא טענה אינדוקטיבית (invariant
שמורה)
, נמצא טענה אינדוקטיבית (invariant
שמורה) ![plot:\[{I_l}\left( {\bar x} \right)\]](/documentResources/326/plot_183.png) . כמו כן, תמיד נבחר:
. כמו כן, תמיד נבחר: 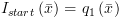 ,
, 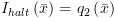 .
.
- לכל מסלול
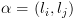 שלא עובר דרך נקודות חתך
אחרות נוכיח את תנאי הנכונות:
שלא עובר דרך נקודות חתך
אחרות נוכיח את תנאי הנכונות:![plot:${I_l}_i\left( {\bar x} \right)
\wedge {R_\alpha }\left( {\bar x} \right) \to {I_l}_j\left[ {\bar x
\leftarrow {T_\alpha }\left( {\bar x} \right)} \right]$](/documentResources/326/plot_577.png) .
.
(אם מתקיים התנאי הראשון על המשתנים בנקודה הראשונה וגם המסלול עביר אז
יתקיים התנאי השני על הטרנספורמר של המסלול על המשתנים).
אם הפעלנו את הכלל בהצלחה נסמן: ![plot:\[{ \vdash _F}\left\{ {{q_1}} \right\}P\left\{ {{q_2}} \right\}\]](/documentResources/326/plot_184.png)
הערות:
- כאשר מדובר על
תוכנית עם מעגלים נכונות חלקית ונכונות מלאה לא מתלכדים. כלל Floyd
מוכיח נכונות חלקית בלבד.
- הרעיון מאחורי
בחירת נקודות החתך הוא לדאוג שכל מסלול בין 2 נקודות חתך יהיה סופי.


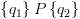 . נשתמש בכלל הבא:
. נשתמש בכלל הבא: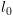
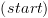 תהיה נקודת חתך.
תהיה נקודת חתך.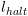
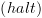 תהיה נקודת חתך.
תהיה נקודת חתך.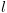 , נמצא טענה אינדוקטיבית (invariant
שמורה)
, נמצא טענה אינדוקטיבית (invariant
שמורה) ![plot:\[{I_l}\left( {\bar x} \right)\]](/documentResources/326/plot_183.png) . כמו כן, תמיד נבחר:
. כמו כן, תמיד נבחר: 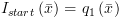 ,
, 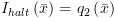 .
.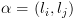 שלא עובר דרך נקודות חתך
אחרות נוכיח את תנאי הנכונות:
שלא עובר דרך נקודות חתך
אחרות נוכיח את תנאי הנכונות:![plot:${I_l}_i\left( {\bar x} \right)
\wedge {R_\alpha }\left( {\bar x} \right) \to {I_l}_j\left[ {\bar x
\leftarrow {T_\alpha }\left( {\bar x} \right)} \right]$](/documentResources/326/plot_577.png) .
. ![plot:\[{ \vdash _F}\left\{ {{q_1}} \right\}P\left\{ {{q_2}} \right\}\]](/documentResources/326/plot_184.png)
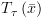 ושל
ושל