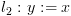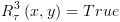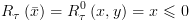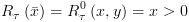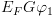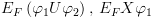4.4.3. הגדרה אינדוקטיבית של 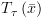 ושל
ושל 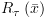
יהי מסלול 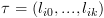 . נחשב סדרה של ביטויים
. נחשב סדרה של ביטויים 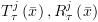 על המסלול מהסוף להתחלה,
כלומר נתחיל ב-
על המסלול מהסוף להתחלה,
כלומר נתחיל ב-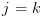 ונסיים ב-
ונסיים ב-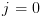 .
.
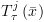 מציין את טרנספורמצית המצבים על המסלול
מציין את טרנספורמצית המצבים על המסלול 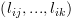
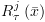 הינו תנאי הישיבות המסלול
הינו תנאי הישיבות המסלול 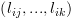
הערה: צריך לשים לב שכאשר אנחנו מסתכלים
על חישוב מסלול, החישוב 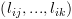 אינו כולל את ביצוע הפקודה הרשומה ב-
אינו כולל את ביצוע הפקודה הרשומה ב-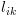 .
.
בסיס ההגדרה: 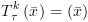 ,
, 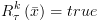
הסבר:
בשלב זה המסלול הוא 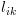 ולכן:
ולכן:
- המשתנים בסיום
זהים למשתנים בהתחלה.
- התנאי למעבר
הוא
 .
.
צעד האינדוקציה: בהינתן 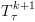 ,
, 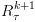 נרצה לחשב
נרצה לחשב 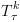 ,
, 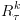 .
.
א. הצבה: 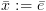 :
: ![plot:$\begin{gathered}
R_\tau ^k\left( {\bar x} \right) =
R_\tau ^{k + 1}\left[ {\bar x \leftarrow \bar e} \right] \hfill \\
T_\tau ^k\left( {\bar x} \right) =
T_\tau ^{k + 1}\left[ {\bar x \leftarrow \bar e} \right] \hfill \\
\end{gathered} $](/documentResources/326/plot_515.png)
ב. תנאי : 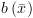 : אם
זה הצד החיובי של התנאי:
: אם
זה הצד החיובי של התנאי: 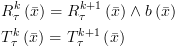
אם זה הצד השלילי של
התנאי: 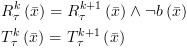
אופן החישוב: נחשב את 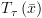 ואת
ואת 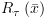 ע"י חישוב "אחורנית": בהינתן מסלול
ע"י חישוב "אחורנית": בהינתן מסלול 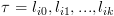 נתחיל עם
נתחיל עם ![plot:\[T_\tau ^k\left( {\bar x} \right)\]](/documentResources/326/plot_180.png) ונסיים עם
ונסיים עם ![plot:\[T_\tau ^0\left( {\bar x} \right)\]](/documentResources/326/plot_181.png) . יתקיים:
. יתקיים: ![plot:\[{T_\tau }\left( {\bar x} \right) =
T_\tau ^0\left( {\bar x} \right)\]](/documentResources/326/plot_182.png) .
.
דוגמא: יהא
תרשים הזרימה הבא:
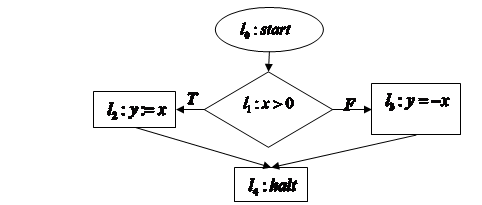
הביטו כעת בטבלה. שימו לב כשאתם קוראים
את הטבלה הבאה שבנייתה החלה מ-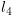 ונמשכה כלפי מעלה אל הצמתים הראשונות. באפור –
המסקנות אליהן אנו מגיעים.
ונמשכה כלפי מעלה אל הצמתים הראשונות. באפור –
המסקנות אליהן אנו מגיעים.


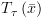 ושל
ושל 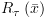
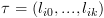 . נחשב סדרה של ביטויים
. נחשב סדרה של ביטויים 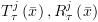 על המסלול מהסוף להתחלה,
כלומר נתחיל ב-
על המסלול מהסוף להתחלה,
כלומר נתחיל ב-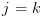 ונסיים ב-
ונסיים ב-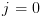 .
.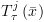 מציין את טרנספורמצית המצבים על המסלול
מציין את טרנספורמצית המצבים על המסלול 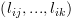
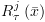 הינו תנאי הישיבות המסלול
הינו תנאי הישיבות המסלול 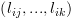
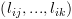 אינו כולל את ביצוע הפקודה הרשומה ב-
אינו כולל את ביצוע הפקודה הרשומה ב-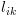 .
.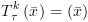 ,
, 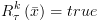
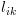 ולכן:
ולכן: .
.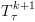 ,
, 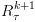 נרצה לחשב
נרצה לחשב 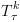 ,
, 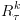 .
.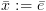 :
: ![plot:$\begin{gathered}
R_\tau ^k\left( {\bar x} \right) =
R_\tau ^{k + 1}\left[ {\bar x \leftarrow \bar e} \right] \hfill \\
T_\tau ^k\left( {\bar x} \right) =
T_\tau ^{k + 1}\left[ {\bar x \leftarrow \bar e} \right] \hfill \\
\end{gathered} $](/documentResources/326/plot_515.png)
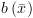 : אם
זה הצד החיובי של התנאי:
: אם
זה הצד החיובי של התנאי: 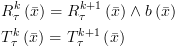
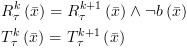
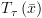 ואת
ואת 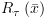 ע"י חישוב "אחורנית": בהינתן מסלול
ע"י חישוב "אחורנית": בהינתן מסלול 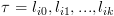 נתחיל עם
נתחיל עם ![plot:\[T_\tau ^k\left( {\bar x} \right)\]](/documentResources/326/plot_180.png) ונסיים עם
ונסיים עם ![plot:\[T_\tau ^0\left( {\bar x} \right)\]](/documentResources/326/plot_181.png) . יתקיים:
. יתקיים: ![plot:\[{T_\tau }\left( {\bar x} \right) =
T_\tau ^0\left( {\bar x} \right)\]](/documentResources/326/plot_182.png) .
.
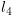 ונמשכה כלפי מעלה אל הצמתים הראשונות. באפור –
המסקנות אליהן אנו מגיעים.
ונמשכה כלפי מעלה אל הצמתים הראשונות. באפור –
המסקנות אליהן אנו מגיעים.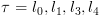 מסלול ימני
מסלול ימני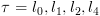 מסלול שמאלי
מסלול שמאלי
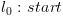
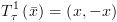
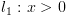
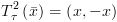
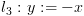
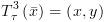
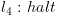
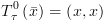
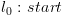
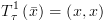
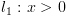
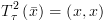
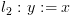
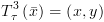
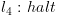
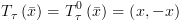
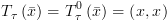
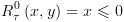
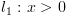
![plot:$R_\tau ^2\left( {x,y} \right) =
True\left[ {y \leftarrow - x} \right]
= True$](/documentResources/326/plot_547.png)
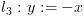
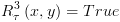
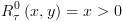
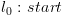
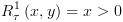
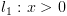
![plot:$R_\tau ^2\left( {x,y} \right) =
True\left[ {y \leftarrow x} \right] = True$](/documentResources/326/plot_555.png)